SOLUTION: Rewrite the system of equations as an augmented matrix. Then simplify the matrix to reduced row echelon form. Identify the solution to the system of equations; x + y + z = 3

Algebra ->  Matrices-and-determiminant -> SOLUTION: Rewrite the system of equations as an augmented matrix. Then simplify the matrix to reduced row echelon form. Identify the solution to the system of equations; x + y + z = 3       Log On


   

Question 592297: Rewrite the system of equations as an augmented matrix. Then simplify the matrix to reduced row echelon form. Identify the solution to the system of equations;
x + y + z = 3
2x - y + z = 2
4x - 2y + 3z = 5
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
  x +  y +  z = 3
 2x -  y +  z = 2
 4x - 2y + 3z = 5

 1x + 1y + 1z = 3
 2x - 1y + 1z = 2
 4x - 2y + 3z = 5



The idea is to use row operations to get it to this form 

Add -2Śrow1 to 1Śrow2 to get a 0 where the 2 is on the left
of row2:

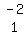
matrix%283%2C1%2C-2%2C1%2C%22%22%29 = 

Add -4Śrow1 to 1Śrow3 to get a 0 where the 4 is on the left
of row3:

matrix%283%2C1%2C-4%2C%22%22%2C1%29 = 

Add 1Śrow2 to 3Śrow1 to get a 0 where the 1 is on row1 2nd elementt

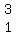
matrix%283%2C1%2C3%2C1%2C%22%22%29 = 

Add -2Śrow2 to 1*row3 to get a 0 where the -6 is:

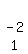
matrix%283%2C1%2C%22%22%2C-2%2C1%29 = 

Add -2Śrow3 to 1*row1 to get a 0 where the 2 is:

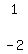
matrix%283%2C1%2C1%2C%22%22%2C-2%29 = 

Add 1Śrow3 to 1*row2 to get a 0 where the -1 is:

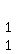
matrix%283%2C1%2C%22%22%2C1%2C1%29 = 

We have all the 0's placed, so all we need do is get the 1's

Get a 1 where the first 3 on row1 is by dividing R1 by 3
Get a 1 where the first -3 on row2 is by dividing R2 by -3
matrix%283%2C1%2C%22%F73%22%2C%22%F7-3%22%2C%22%22%29 = 

This is the row-reduced echelon form.  To get the solution, translate
it into a system of 3 equations and 3 variables:

 1x + 0y + 0z = 1
 0x + 1y + 0z = 1
 0x + 0y + 1z = 1

or

x = 1
y = 1
z = 1

So the solution is (x,y,z) = (1,1,1)

Edwin