SOLUTION: How do you find the side lengths of a triangle when you have the perimeter OR the area, and the ratios of the sides. Example of a problem. Triangle ABC. AB has a scale of 2. BC has

Algebra ->  Triangles -> SOLUTION: How do you find the side lengths of a triangle when you have the perimeter OR the area, and the ratios of the sides. Example of a problem. Triangle ABC. AB has a scale of 2. BC has      Log On


   

Question 590102: How do you find the side lengths of a triangle when you have the perimeter OR the area, and the ratios of the sides. Example of a problem. Triangle ABC. AB has a scale of 2. BC has a scale of 4 and CA has a scale of 5. The area of the triangle is 450 cm2.
Thanks.
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
AB has a scale of 2. BC has a scale of 4 and CA has a scale of 5.
Let k be the constant that you have to multiply 2 by to get the length of AB,
4 by to get the lebnth of BC, and 5 by to get the kength of CA 

AB = 2k, BC = 4k, CA = 5k

Now we use Heron's formula for the area:

Area = sqrt%28s%2A%28s-a%29%2A%28s-b%29%2A%28s-c%29%29

a = AB = 2k, b = BC = 4k, c = CA = 5k

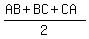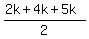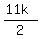s = semiperimeter = %28a%2Bb%2Bc%29%2F2 = %28AB%2BBC%2BCA%29%2F2 = %282k%2B4k%2B5k%29%2F2 = %2811k%29%2F2

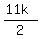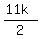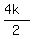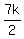s-a = %2811k%29%2F2-2k = %2811k%29%2F2-%284k%29%2F2 =7k%2F2

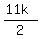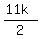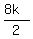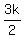s-b = %2811k%29%2F2-4k = %2811k%29%2F2-%288k%29%2F2 =3k%2F2

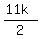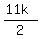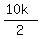s-c = %2811k%29%2F2-5k = %2811k%29%2F2-%2810k%29%2F2 =k%2F2

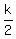Substituting in

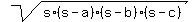Area = sqrt%28s%2A%28s-a%29%28s-b%29%28s-c%29%29

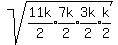450 = sqrt%28expr%2811k%2F2%29%2Aexpr%287k%2F2%29%2Aexpr%283k%2F2%29%2Aexpr%28k%2F2%29%29

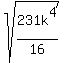450 = sqrt%28231k%5E4%2F16%29

Square both sides:

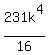202500 = 231k%5E4%2F16

Multiply both sides by 16

3240000 = 231k4

Divide both sides by 231

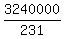3240000%2F231 = k4

Take fourth roots of both sides:

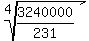root%284%2C3240000%2F231%29 = k

10.88261481 = k

AB = 2k = 2(10.88261481) = 21.76522962 
BC = 4k = 4(10.88261481) = 43.53045924 
CA = 5k = 5(10.88261481) = 54.41307405

[It's much easier if you are given the perimeter instead of the area]

Edwin