Question 590079: 7n^2+11n-6
I need help with polynomials i try so hard but i just dont get it.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I am puzzled at what you expect for an answer, but will give you one anyway.
In the future, your chances for an answer
will depend on asking more specific questions.
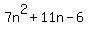 is a polynomial. is a polynomial.
It is made up of 3 terms added up:  , , 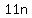 , and , and  . .
A term is an expression that does not involve addition (or subtraction, which is really addition of something with a minus sign).
Because it has three terms, I can call it a trinomial. (If it had 3 wheels, I would call it a tricycle).
It has only one variable: n.
The variable appears with exponents 2, 1, and zero (if I count  as as because because  . .
We always write polynomials starting with the term of highest exponent and going down.
Because the exponent of the variable is the degree,  is the second degree term. is the second degree term.
Because the term of highest degree is  and had degree 2, the polynomial is said to have degree 2. and had degree 2, the polynomial is said to have degree 2.
Polynomials of degree 2 are also called quadratic polynomials. (polynomials of degree 3 are called cubic.
Polynomials graph as wavy lines in their middle part, but run out of the paper at the ends, like this:
 The values of the variable (plotted on the horizontal axis) where the htaph crosses the axis make the polynomial zero, and are called zeros of the polynomial. The values of the variable (plotted on the horizontal axis) where the htaph crosses the axis make the polynomial zero, and are called zeros of the polynomial.
Polynomials are not required to have any zeros that are real numbers. Polynomials of degree 2, 4, 6, ... (even degrees) are allowed to stay on one side of the horizontal axis (usually called the x axis), and if they do they would have no zeros.
Polynomials of odd degree are required to cross the x xis and have at least one zero.
A polynomial can have as many zeros as its degree.
A polynomial that has one or more zeros can be written as a product of 2 or more factors. We call that factoring the polynomial.
The reverse is also true: if you can factor the polynomial, it will have at least as many zeros as one less than the number of factors.
When factoring, you first look for common factors as in
 and and 
Factoring polynomials beyond that is an art, with many tips and tricks and requires practice. It's like playing he piano.
A polynomial with only 2 terms is called a binomial. If its degree is 1 (as in 2x+3, it is also called linear.
A polynomial with only 1 term is not much of a polynomial, but we may allow it to join the other guys, an call it a polynomial by extension. Usually, we call it a monomial.
The product of two binomials is a quadratic trinomial, as in
 . .
The product has all the possible combinations of one term from one binomial and one term from the other binomial.
Tpo make sure we don't forget any product we use a mental checklist that we remember by the acronym FOIL. FOIL stands for First, Outside, Inside, Last. We make sure to include the product of the two First terms from each binomial, the product from the terms that appear om the Outside of the product, the terms that appear on the Inside of the product, and the product of the Last termsfrom each binomial.
In the end we "collect like terms" and add the Outside and Inside products into
the degree 1 term.
In any case, you may recognize the F and L products, and that will hwlp you in factoring.
|
|
|