Question 589118: Mongo has 20 coins consisting of nickels and dimes. if the nickels were dimes and dimes were nickels, he would have 50c more than he now has. how many nickels and how many dimes does he have?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE FIFTH GRADER SOLUTION:
He obviously had more nickels than dimes. This must be a good mental math problem.
If I was told to swap all the nickels for dimes and all the dimes for nickels, I would not make all 20 swaps, because it's so much work.
Instead, I would just take the excess nickels and replace them with dimes.
So, if there were eight dimes, I would set aside all eight dimes and eight of the nickels, and I would only work on swapping the extra nickels for dimes. It's far less work.
As each nickel is replaced with a dime, Mongo gains 5 cents, so for him to gain 50 cents means that 10 coins had to be swapped.
The other 10 coins were left alone, because they were equal numbers of nickels and dimes, 5 of each.
It was only those 10 excess nickels that needed to be swapped.
Mongo had started with 5 dimes and 15 nickels.
THE ALGEBRA SOLUTION.
Let n be the number of nickels, and d be the number of dimes.
Mongo has 20 coins consisting of nickels and dimes means 
He now has (in cents) 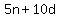 . .
If the nickels were dimes and dimes were nickels, he would have d nickels and n dimes, for a total amount of
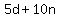 cents. cents.
If the nickels were dimes and dimes were nickels, he would have 50c more than he now has means that

Let's simplify that.
We can subtract 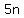 and subtract and subtract 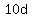 from both sides to get from both sides to get
 --> -->  --> --> 
We can further simplify by dividing both sides by 5
 --> --> 
Now we have a system of equations to solve:

We could "eliminate" d by adding both equations to get
 --> -->  --> --> 
and then substitute  into into  to get to get
 --> -->  --> --> 
|
|
|