|
Question 588700: Hi, I am studying for my college placement test and there is a few math problems that i am having difficulty solving,
1st. square root of 75/2 + cube root of 2/4 =
2nd. 1/2(n^2) - n = 190 my answer was n2-n-380=0 but i think is wrong the answer must equal 0
3rd. 10x^2+5x/5x my answer was 10x^2 but i think is wrong
4th. how to factor 3x^2-15x, the correct answer is 3x(x-5) but i dont know why or how they get those numbers
5th. (4x-7)^2= ? my answer was 16x^2+49 but i think is wrong
Found 2 solutions by KMST, mathhelp@:
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! Once you are accepted, it may not be a bad idea to be placed in a lower level math class, if that class helps you understand math. Of course, that depends on the teacher. Some people believe math is a difficult subject, mastered by memorizing formulas and procedures. I believe math is about understanding the meaning (and memorizing) a few definitions, and using your own reasoning to get the rest.
1)  = ?
For roots, the root of a product equals the product of the roots, and the root of a quotient is the quotient of the roots.
 and  , but those expressions are not the simplified forms expected.
To make things simple (and pretty), we do a lot of clever factoring, like
and we do not like roots of any kind of root in denominators.
We could write a first step with roots in denominators and "fix" it later,but we can also fix it before, as in
Then, 
So 
EXPLANATIONS ADDED:
2) (1/2)n^2 - n = 190 can be transformed into an equivalent equation by multiplying both sides times 2, and then subrracting 380 from both sides:
 -->  -->  -->  --> 
If you needed to solve it, you could use the quadratic formula, or complete the square, like this:
-->  (adding 1 to both sides)
Then writing the left side as the equivalent square, and adding as indicated on the right side:
 --> 
3) (10x^2+5x)/5x= As you divide or multiply a sum, you do that to every one of the terms added. If something priced 4 dollars and 50 cents is sold at half price , it will cost 2 dollars and 25 cents. You divide by two both parts of the price.
In math class we call that very logical fact "the distribbutive property." It is the basis of the procedures for multiplication that we learn in elementary school. We multiply times a factor a large number by splitting that large number into a sum of smaller numbers, multiplying each samller number times the factor separately, and then adding. When you multiply 21 (20+1) times 4, you multiply the 1 to get 4 and the 2 tens (20) to get 8 tens (80), and then add up.
4) how to factor 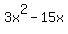 , the correct answer is 3x(x-5)
That is the distributive porperty again:
AND MORE EXPLANATIONS:
5)  = ?
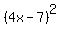The answer is not  .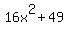
That is just part of the answer, but you are missing something.
If you were to apply the distributive property, you would need to do it twice, like this:
However, algebra students learn what the end result is for a square of a sum, so they do not have to mess with the intermediate steps.
Suppose you have the sum of two expressions, like  and  , but we will call those two expressions A and B, for short. The square of A+B is
You would remember that easier if I draw it
 The surface area of the big square is 
It is made of 2 squares with areas  and  , plus two rectangles, each with area 
So the square of a sum (of two expressions) is the sum of the two squares plus the two rectangles.
So to calculate the square of plus , we add the square of each, plus twice their product
Answer by mathhelp@(10)  (Show Source):
|
|
|
| |
