Question 588237: With a right triangle, if I only know the length of the hypotenuse, what would the formula be for finding the length of the legs?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! If all you have is the length of the hypotenuse, there is no way to find the length of the legs. With that length for the hypotenuse, there is an infinite number of different right triangles.
You could do something if you had some other information, like the mention that this is an isosceles right triangle, or that one of the legs is twice as long as the other, or that the lengths of the legs are certain functions of x, like x+3 and 2x-5. Some information about the angles might help too.
PS:
If the angles are 45, 45, and 90 degrees, the triangle is half of a square.
The two legs are the same length. (That's why we call it isosceles).
All the triangles with angles measuring 45, 45, and 90 degrees are similar, meaning that they have the same shape and the sides lengths have the same ratios. One such triangle is just a scaled up or scaled down version of another.
The length of the hypotenuse is 1.414 times the length of the legs, and the length of the legs is 0.707 times the length of the hypotenuse.
(Those numbers are only good approximations. The exact numbers would be never ending decimals, with infinite number of digits. The exact numbers can only be written as  and  ).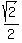
MATH EXPLANATION (optional reading):
Pythagoras theorem says that, in a right triangle, the square of the hypotenuse length equals the sum of the squares of the lengths of the legs.
 Graphically, Pythagoras theorem says that the small squares add to the large square.
In algebra language, Pythagoras says that  -->  and 
For those not yet deep into algebra the squares are defined as
 and  where the middle dots mean multiplied times.
Those squares are the area, in the square units used, of a square of that side length.
From , taking square roots of both sides, you get
From  , taking square roots of both sides, you get
|
|
|
