Question 588217: I have tried to do this question a a lot of time but My answer and the Graph is not coming the Right way... so please help me.
this is the Question:
Concavity of the parabola representing the quadratic function, its y intercept and x intercepts if any exist, and the coordinates of the vertex. sketch the parabola
f(x)=2x^2+4.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
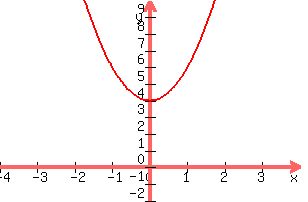
You can put this solution on YOUR website! Concavity of the parabola representing the quadratic function, its y intercept and x intercepts if any exist, and the coordinates of the vertex. sketch the parabola
f(x) = 2x^2 + 4
y = 2x^2 + 4
the y intercept is easy, when x = 0, y = 4 is the y intercept
Find the x intercept, (when y = 0)
2x^2 + 4 = 0
2x^2 = -4
x^2 = -4/2
x^2 = -2
x = 
square root of a negative, no real roots, no x intercept
:
The vertex occurs at the axis of symmetry, equation has no middle term, b=0
therefore the axis of symmetry is 0, hence the vertex, 0, 4
:
If can you plot this equation, it is easy to see
:
x | y
------- 2x^2 + 4 = y; substitute for x, find y
-2 | 12; 2(-2^2) + 4 = 2(4) + 4 = 12
-1 | 6: 2(-1^2) + 4 = 2(1) + 4 = 6
0 | 4; 2(0) + 4 = 4
+1 | 6
+2 |12
:
|
|
|