SOLUTION: How do you get 1.645 when If you use a 0.10 level of significance in a (two-tail) hypothesis test, what is your decision rule for rejecting a null hypothesis that the popu

Algebra ->  Probability-and-statistics -> SOLUTION: How do you get 1.645 when If you use a 0.10 level of significance in a (two-tail) hypothesis test, what is your decision rule for rejecting a null hypothesis that the popu      Log On


   

Question 588065: How do you get 1.645 when
If you use a 0.10 level of significance in a (two-tail) hypothesis test, what is your decision rule for rejecting a null hypothesis that the population mean is 500 if you use the Z test?
What is the formula and how would I get to 1.645?

Answer by Edwin McCravy(20059) About Me  (Show Source):
You can put this solution on YOUR website!


The left-most green line is erected where z=-1.645. 

The right-most green line is erected where z=+1.645. 

The area bounded by the curve, the z-axis, and those two green lines is 90% of
the total area between the curve and the z-axis.  The area to the left of the
left green line is 5% of the total area, and the area to the right of the right
green line is the other 5% of the total area between the curve and the z-axis.

Your are testing the hypothesis 

H0:  m = 500

against the alternative hypothess

Ha:  m ≠ 500
 
Suppose you took a sample of size n=100 and 
found that the sample mean was ⴳ = 493 and
the standard deviation were s = 50

Then you would calculate this test statistic:

     ⴳ - m 
z = 覧覧覧覧
       s%2Fsqrt%28n%29


      493 - 500 
z = 覧覧覧覧覧覧 = -1.4
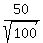         50%2Fsqrt%28100%29

This would correcpond to the red line drawn
at -1.4



and since the 1.4 value of z is between the
two green bars, the mean of 493 is close
enough to 500 with a sample that size with that
standard deviation, and so we would fail to
reject the hypothesis.

However, suppose you took a sample of size n=64 and 
found that the sample mean was ⴳ = 495 and
the standard deviation were s = 20
Then you would calculate this test statistic:

     ⴳ - m 
z = 覧覧覧覧
       s%2Fsqrt%28n%29

      495 - 500 
z = 覧覧覧覧覧覧 = -2.0
         20%2Fsqrt%2864%29
This would correcpond to the red line drawn
at -2.0

and since the 2.0 value of z is NOT between the two green bars, the mean of 495
with a sample that size with that standard deviation, is not close enough to
500, and so we would reject the null hypothesis.

Notice that a lot depends on the size and the standard deviation of the sample we take.

Now since this is a 2-tail test, the sample mean could be larger than 500

Suppose you took a sample of size n=81 and 
found that the sample mean was ⴳ = 510 and
the standard deviation were s = 70
Then you would calculate this test statistic:

     ⴳ - m 
z = 覧覧覧覧
       s%2Fsqrt%28n%29

      510 - 500 
z = 覧覧覧覧覧覧 = -1.29
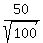         50%2Fsqrt%28100%29

This would correcpond to the red line drawn
at -1.29

and since the 1.29 value of z is between the
two green bars, the mean of 510 is close
enough to 500 with a sample that size with that
standard deviation, and so we would fail to
reject the hypothesis.

However, suppose you took a sample of size n=150 and 
found that the sample mean was ⴳ = 506 and
the standard deviation were s = 40
Then you would calculate this test statistic:

     ⴳ - m 
z = 覧覧覧覧
       s%2Fsqrt%28n%29

      506 - 500 
z = 覧覧覧覧覧覧 = 1.84
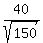         40%2Fsqrt%28150%29

This would correcpond to the red line drawn
at +1.84

and since the 1.84 value of z is NOT between the two green bars, the mean of 506
with a sample that size with that standard deviation, is not close enough to
500, and so we would reject the null hypothesis.

Edwin