Question 586501: What is the area of a 20-gon with a radius of 2 mm? Please explain.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! Inside a circle with a radius of 2mm, a 20-sided regular polygon is inscribed.
Each of the 20 vertices is on the circuference of the circle, at 2 mm from the center.
Since the polygon is a regular 20-gon, all the sides an angles have the same measure, and you could connect all the vertices to the center and split that 20-gon into 20 isosceles triangles with 2mm legs.
As we are splitting, let's draw a line from the middle of each side to the center, spiltting each isosceles triangle into 2 right triangles.
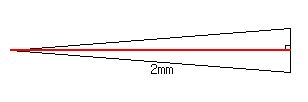 This is one of those little isosceles triangles, magnified.
Each of those 40 right triangles has a  angle at the center, and a 2mm long hypotenuse.
We can calculate the length of the legs of those triangles with trigonometric functions.
The short leg, opposed to the angle is half of the side of the 20-gon. We can consider it to be the base of the tiny right triangle, and its measure, in mm, is
 .
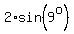The length of the long leg, the height of the tiny right triangle, can be calculated as
 .
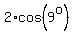The area of each of those 40 right triangles, in square millimeters, would be
That's approximaterly 0.309 (((mm^2}}}
The area of the 20-gon, made up of 40 of those little right triangles, will be
|
|
|
