Matt flipped two fairs coins together. He continued doing so until at least one of the coins turns up heads. What is the probability that both are heads on the last flip? please explain
This could theoretically go on forever and Matt never get anything but tails.
So it is a infinite geometric series of probabilities.
He will always either get HH, HT, TH, or TT, each with probability of  .
To succeed, Matt must get HH on the first throw or get only TT successively
a bunch of times and then HH on the final throw.
So we want the probability of:
1. HH 1st time with probability
.
To succeed, Matt must get HH on the first throw or get only TT successively
a bunch of times and then HH on the final throw.
So we want the probability of:
1. HH 1st time with probability  OR
2. TT 1st time and HH 2nd time with probability
OR
2. TT 1st time and HH 2nd time with probability  ·
· =
= 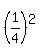 OR
3. TT 1st 2 times and HH 3rd time with probability
OR
3. TT 1st 2 times and HH 3rd time with probability 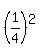 ·
· =
= 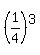 OR
4. TT 1st 3 times and HH 4th time with probability
OR
4. TT 1st 3 times and HH 4th time with probability 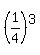 ·
· =
= 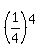 OR
...
OR means "add", so the desired probability is the sum of this infinite
geometric series:
OR
...
OR means "add", so the desired probability is the sum of this infinite
geometric series:
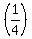 +
+ 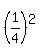 +
+ 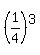 +
+ 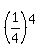 + ...
the formula for which is
+ ...
the formula for which is
 =
= 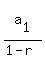 where
where  = r =
= r = 
 =
= 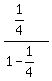 =
= 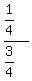 =
= 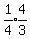 =
= 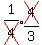 =
=  Edwin
Edwin