Question 582260: Mr. Stewart rode a distance of 12 miles into the country on a bicycle and returned on foot. His rate on the bicycle was 4 times his rate on foot. The entire trip took 5 hours. How long did he travel?
I am not sure how to set up this problem...
Found 2 solutions by mananth, KMST:
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! walking speed = x
cycle speed = 4x
distance = 12 miles
time walking + time cycling = 5 hours
12/x + 12/4x= 5
12/x + 3/x= 5
15/x=5
x= 15/5
x=3 miles / hour walking speed
4x= 4*3 = 12 mph cycling speed
He walked for 12/3 = 4 hours
he bicycled for 12/12 = 1 hour.
I think you have to change the question.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is a weird problem, with an unexpected, unclear question.
Is the problem asking for the length of the total trip in miles? Is it asking for the total time it took in hours? Is it asking how long it took (in hours) for Mr. Stewart to bike to the country and/or to walk back? Should the problem be asking how fast Mr. Stewart walks and/or how fast he can ride a bicycle?
Mr. Stewart traveled 12 miles into the country and 12 miles back, so I would say he traveled a total of 24 miles (12 miles + 12 miles = 24 miles).
Mr. Stewart's entire trip took 5 hours. The problem says so.
As for the other possible meanings of the question, I would set up a variable or two. If you are studying systems of equations, two variables may be expected, but you can solve it with just one.
Probably time for each leg of the trip is what's asked for. That would be very easy for a fifth grader, but we get so smart with algebra that we are not smarter than a fifth grader.
THE ALGEBRA SOLUTION.
Let x be the time Mr. Stewart spent biking into the country, in hours.
(If you need a second variable, make y the time he spent walking back).
Mr. Stewart's biking speed in miles per hour is  . .
Mr. Stewart's walking speed in miles per hour is 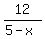
(or walking speed =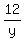 and and  , if using two variables) , if using two variables)
Now we use the fact that he bikes 4 times faster than he walks:

(or  if using two variables). if using two variables).
We solve (with one variable):
 --> -->  (dividing both sides by 12) (dividing both sides by 12)
 --> -->  --> -->  --> --> 
So Mr. Stewart biked for 1 hour and walked for 4 hours.
(With 2 variables,  --> -->  --> -->  , and the system , and the system
 gets solved into gets solved into  and and  ). ).
FIFTH GRADER SOLUTION
If Mr. Stewart bikes 4 times faster than he walks, it must have taken him 4 times as long to walk back. So for every hour biking, he would need 4 hours walking for a total time of 5 hours for the round trip. So the answer is that exactly that is what happened. He biked 1 hour into the country. There he returned the bike he had borrowed early yesterday evening, and he had to walk back for 4 hours. He did not mind, because it was such a fine, cool Spring morning.
|
|
|