Question 582155: According to Newton's universal gravitation, the attractive force F between two bodies is given by

where m1 and m2 are the mass of the two bodies, r is the distance between the two bodies, and G is the gravitational constant = 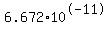 newtons meter squared kilogram squared. newtons meter squared kilogram squared.
Suppose an object is traveling directly from Earth to the moon. The mass of Earth is 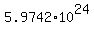 kilograms, the mass of the moon is kilograms, the mass of the moon is 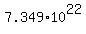 kilograms, and the mean distance from Earth to the moon is 384000 kilometers. For an object between Earth and the moon, how far from Earth is the force on the object due to the moon greater than the force on the object due to Earth? kilograms, and the mean distance from Earth to the moon is 384000 kilometers. For an object between Earth and the moon, how far from Earth is the force on the object due to the moon greater than the force on the object due to Earth?
Thank you!
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! Suppose d is the distance between this object and Earth, m_1 is the mass of the object, m_2 and m_3 are the masses of the Earth and moon, respectively. Then r-d or 384000-d is the distance between the object and the Moon. We want the following inequality to be true:
^2})
G and m_1 cancel, leaving
^2} \Rightarrow m_2 (r-d)^2 < m_3 d^2 \Rightarrow m_2 (r-d)^2 - m_3 d^2 < 0)
Since m_2, m_3, and r are known, solve the quadratic in terms of d (you will have to expand, simplify first), replace m_2, m_3, r in, and find the smallest d such that the gravitational force from the Moon is greater than the force from the Earth.
|
|
|