Question 581931: This is a derivative minimum word problem.
It says first find the function f(x)that we want to maximize or minimize. Then differentiate to get the derivative of f(x). Then solve the derivative equal to zero to get the solution. The question I have is.
A box with rectangular sides, base and top is to have a volume of 4 cubic feet. It has a square base. If the material for the base and top costs $10 /ft^2 and the sides costs $20/ft^2 what is the least cost it can be made for?
Every time I have a question of squares, rectangles etc. I am Completely confused.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the length of the sides of the square base, in feet, be x.
The surface area of the base is  square feet. square feet.
The volume is the area of the base,  , times the height , h. , times the height , h.
So,
 <--> <--> 
The surface area of the sides can be calculated as perimeter of the base,  times height, times height, 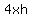 , and substituting the expression for h found above: , and substituting the expression for h found above:
lateral surface =  (in square feet) (in square feet)
The cost for base and top, in $, is

The cost for the sides is

Total cost is

 , which is zero for , which is zero for 

The derivative is zero for  , negative for x<2, and positive for x>2, indicating a minimum of , negative for x<2, and positive for x>2, indicating a minimum of 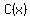 at at  , and that minimum cost is , and that minimum cost is 
|
|
|