SOLUTION: The product of two consecutive positive integers is 142 more than the next integer.What is the largest of the three integers?

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: The product of two consecutive positive integers is 142 more than the next integer.What is the largest of the three integers?      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 58165: The product of two consecutive positive integers is 142 more than the next integer.What is the largest of the three integers?
Answer by hayek(51) About Me  (Show Source):
You can put this solution on YOUR website!
Integer 1: x
Integer 2: y
Integer 3: z
----
We know we have three consequtive integers, so:
x=x
y=x+1
z=x+2
-------
"product of two consecutive positive integers" ==> 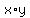x%2Ay
"is 142 more than the next integer"==> =z%2B142
---
So, the equation is: x%2Ay=z%2B142
Now, substitute the equations for x, y, and z from above:
x%2A%28x%2B1%29=%28x%2B2%29%2B142
Solved by pluggable solver: EXPLAIN simplification of an expression
Your Result:


YOUR ANSWER


  • This is an equation! Solutions: x=12,x=-12.
  • Graphical form: Equation x%2A%28x%2B1%29=%28x%2B2%29%2B142 was fully solved.
  • Text form: x*(x+1)=(x+2)+142 simplifies to 0=0
  • Cartoon (animation) form: simplify_cartoon%28+x%2A%28x%2B1%29=%28x%2B2%29%2B142+%29
    For tutors: simplify_cartoon( x*(x+1)=(x+2)+142 )
  • If you have a website, here's a link to this solution.

DETAILED EXPLANATION

Look at x%2A%28x%2B1%29=highlight_red%28+%28x%2B2%29+%29%2B142.
Remove unneeded parentheses around terms highlight_red%28+x+%29,highlight_red%28+2+%29
It becomes x%2A%28x%2B1%29=highlight_green%28+x+%29%2Bhighlight_green%28+2+%29%2B142.
Look at x%2A%28x%2B1%29=x%2Bhighlight_red%28+2+%29%2Bhighlight_red%28+142+%29.
Added fractions or integers together
It becomes x%2A%28x%2B1%29=x%2Bhighlight_green%28+144+%29.
Look at x%2A%28x%2B1%29=highlight_red%28+x%2B144+%29.
Moved these terms to the left 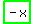highlight_green%28+-x+%29,highlight_green%28+-144+%29
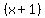
It becomes x%2A%28x%2B1%29-highlight_green%28+x+%29-highlight_green%28+144+%29=0.
Look at highlight_red%28+x%2A%28x%2B1%29+%29-x-144=0.
Expanded term x by using associative property on %28x%2B1%29
It becomes highlight_green%28+x%2Ax+%29%2Bhighlight_green%28+x%2A1+%29-x-144=0.
Look at x%2Ax%2Bx%2Ahighlight_red%28+1+%29-x-144=0.
Remove extraneous '1' from product highlight_red%28+1+%29
It becomes x%2Ax%2Bx-x-144=0.
Look at highlight_red%28+x+%29%2Ahighlight_red%28+x+%29%2Bx-x-144=0.
Reduce similar several occurrences of highlight_red%28+x+%29 to highlight_green%28+x%5E2+%29
It becomes highlight_green%28+x%5E2+%29%2Bx-x-144=0.
Look at x%5E2%2Bhighlight_red%28+x+%29-highlight_red%28+x+%29-144=0.
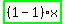
Eliminated similar terms highlight_red%28+x+%29,highlight_red%28+-x+%29 replacing them with highlight_green%28+%281-1%29%2Ax+%29
It becomes x%5E2%2Bhighlight_green%28+%281-1%29%2Ax+%29-144=0.
Look at x%5E2%2Bhighlight_red%28+%281-1%29%2Ax+%29-144=0.
Since highlight_red%28+%281-1%29%2Ax+%29 has zero as a factor, it should be replaced with a zero
Look at x%5E2%2B0-144=0.
Added fractions or integers together
It becomes x%5E2%2B0-144=0.
Look at x%5E2%2Bhighlight_red%28+0+%29-144=0.
Remove extraneous zero highlight_red%28+0+%29
It becomes x%5E2-144=0.
Look at highlight_red%28+x%5E2-144+%29=0.
Equation highlight_red%28+x%5E2-144=0+%29 is a quadratic equation: x^2-144 =0, and has solutions 12,-12
It becomes highlight_green%28+0+%29=0.
Result: 0=0
This is an equation! Solutions: x=12,x=-12.

Universal Simplifier and Solver


Done!

--
We know X is positive, so highlight%28x=12%29 and the remaining integers are 13 and 14.