Question 581154: Please show the steps on how to solve this multiplication problem.
(3 - squarerootof-5) * (1 + squarerootof-1)
(in other words..)
quantity (three minus squareroot of negative five) multiplied by quantity (one plus squareroot of negative one)
answer is in a + bi form and is as follows...
(3 + squarerootof5) + (3 - squarerootof5)i
Thank you so much.
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given to expand:
.
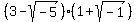
.
Here's a long explanation of this problem that might give you some insight into how you do it.
.
We are going to define a new term i in which i is the square root of -1. We write it as  . That being the case, then if we square both sides of this definition, we also have that . That being the case, then if we square both sides of this definition, we also have that  . With these two definitions in mind we can proceed with this problem step-by-step. . With these two definitions in mind we can proceed with this problem step-by-step.
.
Let's work on how we can replace the  . Recognize that we can replace -5 by 5 times -1. But by our definitions of i we know that . Recognize that we can replace -5 by 5 times -1. But by our definitions of i we know that  So, substitute So, substitute  for -1 and the 5 times -1 becomes for -1 and the 5 times -1 becomes  . .
.
This means that in the first set of parentheses, the term:
.
 can be replaced by can be replaced by 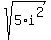
.
Furthermore, under the algebraic rules for square roots, this replacement can be split into two parts as follows:
.

.
But the square root of a squared term, that term being i squared, is just the term itself. So we can replace 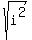 with just i. With this substitution we then get: with just i. With this substitution we then get:
.

.
So going back to the original problem, the contents of the first set of parentheses can be written as:
.
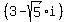
.
It would be a long process to go through this sort of work every time you encounter the square root of a negative number. Instead, you can just use the shortcut of saying "the square root of this negative number, is just the square root of the positive number times i." As an example: for 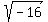 just say it equals just say it equals 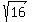 times i. [Note that since the square root of 16 is 4, this can be further reduced to times i. [Note that since the square root of 16 is 4, this can be further reduced to  ] ]
.
With this short cut in mind, let's look at the contents of the second set of parentheses in the original problem, namely 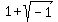 . According to the shortcut, the second term will become just . According to the shortcut, the second term will become just  and since the square root of 1 is just 1, the second term is just 1*i or simply i. (This also matches the definition that and since the square root of 1 is just 1, the second term is just 1*i or simply i. (This also matches the definition that  ). So the second set of parentheses in the problem contains ). So the second set of parentheses in the problem contains 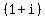 . .
.
We have now converted the original problem to:
.

.
We can now do the multiplication using the FOIL method. To do that, first multiply the 3 in the first set of parentheses times both of the terms in the second set of parentheses to get the product  . Next multiply the second term in the first set of parentheses times both terms in the second set of parentheses. In other words, multiply . Next multiply the second term in the first set of parentheses times both terms in the second set of parentheses. In other words, multiply 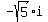 times times 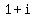 to get to get  . But recall from our definitions that . But recall from our definitions that  . When we replace the . When we replace the  by -1, the contents of this product becomes: by -1, the contents of this product becomes:
.
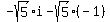
.
And the multiplication by -1 makes it become:
.
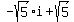
.
Finally, add these two products as follows:
.
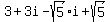
.
The the last step is to put this into conventional form by combining the real parts and combining the imaginary parts (all terms containing i) second. This makes the answer become:
.

.
Factor out i from the last two terms and the result is:
.
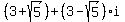
.
and that's the answer that you said we should get.
.
That's the way to do this problem. I hope this gives you some insight into working with complex numbers (numbers having both real and imaginary parts.) It's not too hard, but it takes lots of practice and you need to remember that  and that and that  . .
|
|
|