Question 579322: sorry this is calculus, please help
Given the function f(x)=3cosx for the interval 0
i)determine the values of x for which the function is increasing
ii)find the critical points and determine their nature
iii)determine the concavity of the function, between the critical values
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  is continuous, but it does have maxima and minima. is continuous, but it does have maxima and minima.
To find where the function increases, decreases, or has a maximum or minimum, you need to look at its derivative.
To find curvature, points of inflection, concavity, you need to look at the second derivative.
The first derivative is
f'(x)=
It is zero at  , ,  , ,  , etc , etc
Those would be maxima or minima of f(x).
The derivative is positive when  , ,  , , 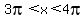 , , 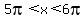 , etc. Those are the intervals where f(x) is increasing. Where , etc. Those are the intervals where f(x) is increasing. Where 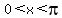 , ,  , the derivative is negative and the function decreases. , the derivative is negative and the function decreases.
Putting it all together, the function increases from  to 0; has a maximum at x=0; decreases from there to to 0; has a maximum at x=0; decreases from there to  ; has a minimum at ; has a minimum at  ; increases from there to ; increases from there to  ; has a maximum at ; has a maximum at  , and so on. The value of the function is , and so on. The value of the function is  at all maxima and at all maxima and  at all minima. at all minima.
The second derivative is f”(x)=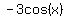 . .
It goes through zero and changes signs at  , ,  , ,  , etc. Those are points of inflection of f(x). The value of the first derivative at those points is either 3 or -3, which gives you the slope of the tangent at those points. , etc. Those are points of inflection of f(x). The value of the first derivative at those points is either 3 or -3, which gives you the slope of the tangent at those points.
The second derivative is negative between  and and  , positive between , positive between  and and  , negative between , negative between  and and 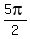 , and so on. As a result the function is concave downwards between , and so on. As a result the function is concave downwards between  and and  , concave upwards between , concave upwards between  and and  , concave downwards between , concave downwards between  and and 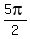 , and so on. , and so on.
|
|
|