SOLUTION: find the value of x in this equation : log(x+3)+log(x-1)=0

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: find the value of x in this equation : log(x+3)+log(x-1)=0      Log On


   

Question 578477: find the value of x in this equation :
log(x+3)+log(x-1)=0
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Logarithm of a product is the sum of the logarithms of the factors, so
log%28%28x%2B3%29%29%2Blog%28%28x-1%29%29=0 --> log%28%28%28x%2B3%29%2A%28x-1%29%29%29=0
The next step is the transformation
log%28%28%28x%2B3%29%2A%28x-1%29%29%29=0 --> %28x%2B3%29%2A%28x-1%29=1
achieved applying antilogarithm (inverse function of logarithm, antilog%28%28y%29%29=10%5Ey) to both sides
10%5Elog%28%28%28x%2B3%29%2A%28x-1%29%29%29=10%5E0 or %28x%2B3%29%2A%28x-1%29=1
From then on, it's a quadratic equation
%28x%2B3%29%2A%28x-1%29=1 --> x%5E2%2B2x-3=1 --> x%5E2%2B2x-4=0
Here we apply the quadratic formula.

The positive solution, x=-1%2Bsqrt%285%29, makes both factors positive:
x-1=-2%2Bsqrt%285%29%3E0 and x%2B3=2%2Bsqrt%285%29%3E0
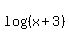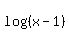log%28%28x%2B3%29%29 and log%28%28x-1%29%29 exist, and
highlight%28x=-1%2Bsqrt%285%29%29 is a valid solution of the original equation.
The negative solution, x=-1-sqrt%285%29, is an extraneous solution.
It makes both factors negative:
x-1=-2-sqrt%285%29%3C0 and x%2B3=2-sqrt%285%29%3C0, and as a consequence
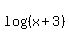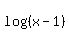log%28%28x%2B3%29%29 and log%28%28x-1%29%29 do not exist for that x value, so it is not a solution of the original equation.