y = x + 3
3x + y = -1
Graph the first line by getting some points:
For the first line, get three points. Choose 3
arbitrary numbers for one letter, substitute them
into the first equation and solve for the other
letter. Them make them into a point (x,y)
Arbitrarily choose 1 to substitute for y
y = x + 3
1 = x + 3
subtract 3 from both sides
-2 = x
plot the point (-2,1)
Arbitrarily choose 0 to substitute for x
y = x + 3
y = 0 + 3
y = 3
plot the point (0,3)
Arbitrarily choose 2 to substitute for x
y = x + 3
y = 2 + 3
y = 5
plot the point (2,5)
Draw a red line through these three points:
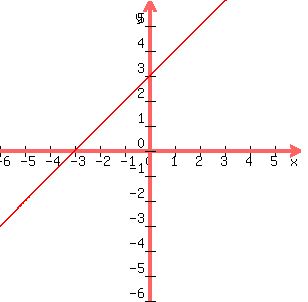Likewise for the second line, get three points.
Arbitrarily choose 5 to substitute for y
3x + y = -1
3x + 5 = -1
subtract 5 from both sides
3x = -6
Divide both sides by 3
x = -2
plot the point (-2,5) on the same graph.
Arbitrarily choose 0 to substitute for x
3x + y = -1
3(0) + y = -1
0 + y = -1
y = -1
plot the point (0,-1)
Arbitrarily choose 1 to substitute for x
3x + y = -1
3(1) + y = -1
3 + y = -1
subtract 3 from both sides
y = -4
plot the point (1,-4)
Draw a green line through these three points:
Now you have this graph:
Notice the the red and green lines cross at the point
which is directly above -1 on the x axis, and which
is directly to the left of 2 on the y-axis.
Therefore the solution is (x,y) = (-1,2) which
means x = -1 and y = 2
Now we check to see if the solution is correct.
We substitute both x = -1 and y = 2 into the first
equation:
y = x + 3
2 = -1 + 3
2 = 2
So the first equation checks. But that is not
enough. We must also substitute both x = -1 and y = 2
into the second equation as well.
3x + y = -1
3(-1) + 2 = -1
-3 + 2 = -1
-1 = -1
That equation checks also, so (-1,2) is the correct
solution.
Edwin
