Question 578037: how do you expand this expression and I know that you use associative property but how do I use it in this sort of expression. please help I am very curious.
thanks
(3x-1)(2x+5)
Found 3 solutions by mananth, solver91311, KMST:
Answer by mananth(16946)   (Show Source): (Show Source):
Answer by solver91311(24713)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There is the practical procedure that everyone uses, and the theory behind it, that few remember or care about.
THE PRACTICAL PROCEDURE
Each factor is a sum of two terms.
In 3x-1, the first term is 3x and the last term is -1.
In 2x+5, the first term is 2x and the last term is 5.
It is accepted that we skip intermediate calculations that are part of the theory, and just write the end result, which is the sum of all 4 possible products of one term from each factor. To make sure all those 4 products are accounted for, we use the acronym or mnemonic FOIL. It stands for:
F _ First=product of first terms - 
O _ Outside=product of terms written on the outside of the product - 
I _ Inside=product of terms written on the inside of the product - 
L _ Last=product of both last terms - 
So we write
 without any more explanations, because when you get to a certain point in algebra you are allowed to skip the steps that you can do in your head, automatically. without any more explanations, because when you get to a certain point in algebra you are allowed to skip the steps that you can do in your head, automatically.
Next we "collect like terms", meaning adding 
So the whole solution would be written as

THE THEORY
The long theoretical explanation for "FOIL" is that you use the distributive property twice.
It goes like this:
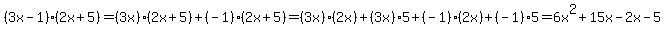
The distributive property is stated, in general terms as
 and we use it, without even thinking about it, each time we multiply a number with two or more digits: and we use it, without even thinking about it, each time we multiply a number with two or more digits:

Incidentally, in  you are also using the distributive property, apparently backwards: you are also using the distributive property, apparently backwards:
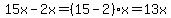
The associative property is the one that says that if you have more that two numbers to multiply, you can multiply any pair first.
So we can calculate 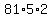 as as  , which gives you the same result, but is much easier that having to multiply 81 times 5 first. , which gives you the same result, but is much easier that having to multiply 81 times 5 first.
I hope you were really so very curious that you enjoyed the long explanation.
|
|
|