SOLUTION: The scores on an exam are normally distributed, with a mean of 77 and a standard deviation of 10. What percent of the scores are greater than 87??

Since 87 is 10, exactly 1 standard deviation, namely 10, above the mean, 
its z-score is 1.  Or we can calulate the z-score by formula:

Calculate the z-score

z = 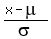 =  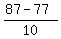=  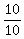= 1.

Anyway we want to find the percentage of area indicated by the
shaded portion below to the right of z=1, which 1 standard deviation
above the mean. 



We are told that the middle region shaded below: 


 
between z=-1 and z=+1 contains about 68.3% of the total
area.  So the rest of the shaded area, which is this,



is 100% - 68.3% = 31.7% of the area, and therefore 
the desired percentage of area, which is this, 
 


is half of 31.7%, and therefore about

15.9% 

Edwin