Question 577747: Two trains leave a city at the same time. One travels North and the other travels South 20mph faster, in 2 hours; the trains are 280 miles apart. Find their rates. (I over slept for my class and I HAVE NO IDEA how to do the assigned homework. This should help me figure the rest of the questions out. Thank you thank you thank you!
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! The basic equation that is used is:
.

.
which we'll shorten to:
.

.
This is pretty straightforward when you think about it. You hop on a bike and ride at 10 mph for 3 hours. How far do you go? 10 mph * 3 hrs = 30 miles of distance.
.
In this train problem we have two separate distances to find because the rates are different. So let's call the train going north Train 1 and the train going south Train 2. (We'll use subscripts to differentiate them.)
.
So, we can write that the distance traveled by Train 1 is:
.

.
and the distance traveled by Train 2 is:
.

.
What else do we know? For one thing we know that both trains travel for 2 hours. Therefore, we can replace both times 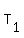 and and  by 2 hrs. by 2 hrs.
.
In addition, we know that the rate for Train 2 is 20 mph more than the rate for Train 1. So we can write:
.

.
Let's make these two substitutions. First, we substitute 2 for both 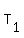 and and  and our two distance equations become: and our two distance equations become:
.
 and and 
.
Then in the equation for 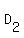 we substitute we substitute  for for  and the equation becomes: and the equation becomes:
.

.
If we then do the distributed multiplication on the right side of this equation by multiplying 2 times each of the quantities in the parentheses, we see that:
.

.
So we now have the two equations:
.
 and and 
.
Finally, what else do we know? Since the trains are going in exactly opposite directions, the distance between them can always be found by adding their distances. So, we can add the two left sides of these equations and similarly add the two right sides to get the equation:
.

.
But we know that the left side of this equation equals 280 miles, the total distance between the two trains. So we replace the left side with 280 and the equation then becomes:
.

.
On the right side of this equation we add the two terms containing 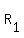 to get: to get:
.

.
Next we get rid of the 40 on the right side by subtracting 40 from both sides as follows:
.

.
and by dividing both sides by 4 we find that:
.

.
We now know that the rate for the train going north (we called it 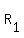 ) is 60 mph. And since we know from the given problem that the rate of the train going south is 20 mph faster, we know that the southbound train is going at the rate of 80 mph. ) is 60 mph. And since we know from the given problem that the rate of the train going south is 20 mph faster, we know that the southbound train is going at the rate of 80 mph.
.
Let's check this, just to help ensure that we didn't make a mistake. At 60 mph in 2 hours the northbound train goes 120 miles. And at 80 mph in the same 2 hours the southbound train goes 160 miles. So the distance between the trains is 120 + 160 = 280 miles, just as the problem says it should be. So, our answers are correct.
.
Hope this helps you with the rest of your problems. Just remember: Distance equals Rate times Time. If you have further questions, just post them and hopefully one of the tutors will be able to give you the assistance you need.
.
Good luck! (And consider getting a louder, more obnoxious sounding alarm clock ... LOL)
|
|
|