SOLUTION: What's the Exact Value for Sin 13π/12 degrees ? Without using a calculator

Algebra ->  Trigonometry-basics -> SOLUTION: What's the Exact Value for Sin 13π/12 degrees ? Without using a calculator       Log On


   

Question 577631: What's the Exact Value for Sin 13π/12 degrees ? Without using a calculator
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
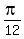
13pi%2F12=pi%2Bpi%2F12 , so our reference angle is pi%2F12
We calculate by reference to angles in the first quadrant whose terminal sides are reflections on the axes or the origin, and whose trigonometric functions have the same absolute value.
The two angles differ by pi or 180%5Eo
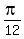pi%2F12 is in the first quadrant, where sine and cosine are positive, while
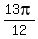13pi%2F12 is in the third quadrant where sine and cosine are negative.
sin%2813pi%2F12%29=-sin%28pi%2F12%29
The only angles in the first quadrant whose trigonometric function values I remember are 0, pi%2F6, pi%2F4, pi%2F3 and pi%2F2 (0, 30, 45, 60, and 90 degrees).
For any other angles, I need those trigonometric identity formulas.
I search for them, and find
sin%28alpha%2F2%29=sqrt%28%281-cos%28alpha%29%29%2F2%29 with a sign to be determined
I know that cos%28pi%2F6%29=sqrt%283%29%2F2
pi%2F12=%28pi%2F6%29%2F2, and both angles are in the first quadrant with positive values for ther trigonometric functions, so

(If there is a way to make it look prettier than that, I do not know it.)
So highlight%28sin%2813pi%2F12%29=-sqrt%282-sqrt%283%29%29%2F2%29