Question 577369: give an example of polynomials p and q of degree 3 such that p(1)=q(1), p(2)=q(2), p(3)=q(3), but p(4) =(not equal) q(4). Show that your polynomials satisfy these conditions.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There is probably a very simple and elegant solution, but I will only see it after I post this messy one,
Consider the function 



There are two many options, but I would try the simplest polynomial function with those three zeros:

I can split  into into 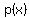 and and 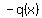 many ways, but I need both polynomials to be of degree 3. many ways, but I need both polynomials to be of degree 3.
I'll try something. There are probably better, simpler ways.
 and and
 made up so that made up so that 

Polynomials p and q are of degree 3
 and and  , so , so 
 and and  , so , so 
 and and  , so , so 
I should not have to prove that, brcause there could only be 3 intersection points for two polynomials of degree 3, but ...
 and and  , so , so  and and 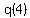 are different. are different.
|
|
|