(-3-3i)(2+2i)
Convert each to trig form:
First we convert -3-3i to trig form:
1. The complex number x+yi is represented by the radius vector (line segment)
from the origin (0,0) to the point (x,y). So draw the radius vector, and
the perpendicular from the point (x,y) to the x-axis.
2. Calculate the length of that vector r, using the Pythagorean theorem:
r²=x²+y². That value is called the modulus of the complex number.
3. Calculate the angle q from the right side of the axis around to the
radius vector. To do this you may use any of the trig ratios involving
x, y and r. This angle is called the argument.
4. Write the trig form as r(cosq + i·sinq)
First we convert -3-3i to trig form:
1. We draw the radius vector connecting the origin to the point (-3,-3) and
the perpendicular from that point to the to the x-axis. We label the
perpendicular to the x-axis as y=-3 and the segment from the origin to
the perpendicular. We label the length of the radius vector r, and
indicate the argument q with a counter-clockwise
arc from the right side of the x-axis around to the radius vector:
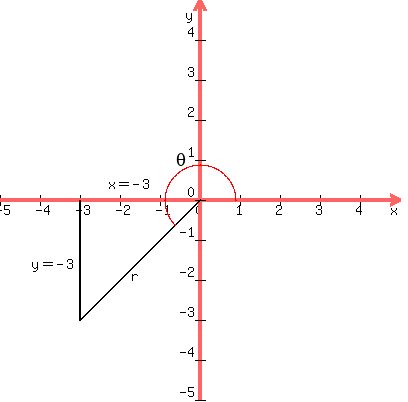2. We calculate the length of that vector r, using the Pythagorean theorem:
r²=x²+y².
r²=(-3)²+(-3)²
r²=9+9
r²=18
r=
r=
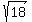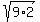r = 3
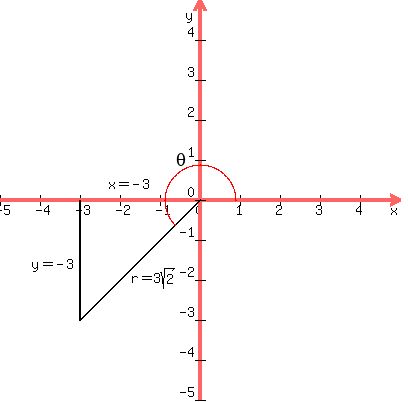3. We calculate the angle q, by realizing that
the right-triangle is a 45°-45°-90° with a reference angle of 45°, and
the actual angle q = 180°+45° = 225°
4. We write the trig form as r(cosq + i·sinq), or
(cos225° + i·sin225°).
---------------
Next we convert 2+2i to trig form:
1. We draw the radius vector connecting the origin to the point (2,2) and
the perpendicular from that point to the to the x-axis. We label the
perpendicular to the x-axis as y=2 and the segment from the origin to
the perpendicular x=2. We label the length of the radius vector r, and
indicate the argument q with a counter-clockwise
arc from the right side of the x-axis around to the radius vector:
2. We calculate the length of that vector r, using the Pythagorean theorem:
r²=x²+y².
r²=(2)²+(2)²
r²=4+4
r²=8
r=
r=
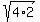r = 2
3. We calculate the angle q, by realizing that
the right-triangle is also a 45°-45°-90° which is an angle of 45°
4. We write the trig form as r(cosq + i·sinq), or
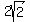(cos45° + i·sin45°).
-----------------
Now we use the formula for multiplying complex numbers in trig form:
r1(cosq1 + i·sinq1)·r2(cosq2 + i·sinq2) = r1r2[cos(q1+q2) + i·sin(q1+q2)].
So we have:
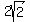(-3-3i)(2+2i) = (cos225° + i·sin225°)·(cos45° + i·sin45°) =
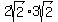[cos(225°+45°) + i·sin(225°+45°)] = 6·2[cos270° + i·sin270°] =
12(cos270° + i·sin270°).
Edwin
