|
Question 575820: The sum of two positive numbers is 640, what should the numbers be if their product is as large as possible?
I really don't even know how to approach this problem. I started off by writing: x+2x=640. I don't know if that is the right way to approach the problem being that I keep getting it wrong when I try and submit the answer. Please help-Thank you :)
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! It's sort of a trick problem.
If your numbers are x and y.
 --> 
The product can be written as a function of x alone:
You want to find the maximum value for that product.
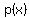 is a quadratic function.
You may be studying quadratic functions, which graph as parabolas.
Do you know all about them and how to find the x for the maximum? If not, read on.
The book probably says that the general form is  , and in your case a=-1, b=640 and c=0.
If the term in  has a positive coefficient (a>0), the parabola looks like a smile, opening up, and going through a minimum at its vertex, somewhere in the middle, like this:  ,
but a minus sign in front of the (a<0) makes it frown like this 
and then there is a maximum at the vertex.
Where is the maximum for  ?
If you are studying quadratic functions, you may be expected to invoke a formula that says that the axis of symmetry and x coordinate of the vertex/maximum is given by
 where b is the coefficient of x and a is the coefficient of .
In this case it would be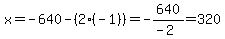 
Otherwise, you may be expected to transform the function like this:
and then say that since the square will be positive or zero, and it has that minus sign in front, the function will be 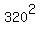 when xthe parenthesis is zero (x=320), and it will be less for any other x value.
Either way, you show that to make the product greatest one of the numbers has to be  ,
and since they add up to 640, the other number is 320 too.
, so 
When the problem said "two positive numbers" you probably assumed they were two different numbers. The problem did not say they were different. That's the trick.
If two numbers have to add up to some constant, their product will be maximum when they are the same number.
Similar problems talk about the perimeter of a rectangle, which is the sum of length plus width, doubled. If the perimeter of a rectangle has to be a certain number, the area will be maximum when length and width are the same, meaning that the rectangle is a square.
|
|
|
| |
