Question 575111: If the area of an isosceles triangle is x sq. cm and each of the congruent sides measures y cm, find the measure of its base?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! It would be a much easier problem if it was an isosceles right triangle.
If you inadvertently left the word "right" out of your posting, I forgive you, but you will habv e to figure out the easier answer.
Other wise, read on.
I saw two "simple" ways to get to the answer. Either one is a nightmare for error prone people like me. (And I don't even want to think of how to work law of sines and/or law of cosines into a solution).
You could use Heron's formula relating the area of a triangle to the lengths of the sides.
You could also use the formula to calculate the area of a triangle having the lengths of two sides and the measure of the included angle.
I like the second option, because I can better visualize the meaning of my calculations.
If the length of the base is B and the measure of the vertex angle is B,
So  and 
Then, either  or 
because usually there are two possible triangles for the same area and leg length.
The maximum area for isosceles triangles of leg length y will happen when sin(B)=1, meaning that it is an isosceles right triangle, and  .
Unless  , there will be two possible triangles, an acute one and an obtuse one, that will have the same sin(B) for vertex angle B.
Because the altitude to the vertex splits the isosceles triangles into two right triangles with hypotenuse y, and a leg of length b/2 opposite an angle of measure B/2,
 and 
At this point, I consult a table of trigonometric identities and find that
 (For a general angle B, there could be a minus sign, but not in this case).
So, substituting into the expression for b,
Next we substitute the expression for cosB found before:
 =  =  =  = 
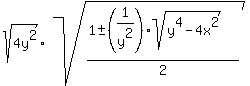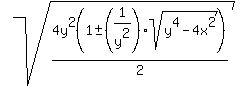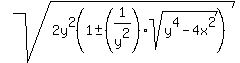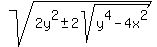
So 
|
|
|
