Question 574997: Sketch the region enclosed by y = e^{3x}, y=e^{7x} and x=1.
Decide whether to integrate with respect to x or y, and then find the area of the region.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! At x=0, y=1 for both functions, so they intersect at (0,1). The region would have vertical line x=1 and the two functions as boundaries. The region has the graph of  as the upper boundary for y, and the graph of as the upper boundary for y, and the graph of  as its lower boundary throughout the [0,1] interval. as its lower boundary throughout the [0,1] interval.
Integrating with respect to x would simply mean
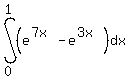
If we try to integrate with respect to y, we need to do some calculations first:
 and and  intersect at (1, intersect at (1, ), and ), and
 and and  intersect at (1, intersect at (1,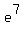 ) )
The y values for the region range between 1 and 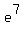
The inverse of  is is  , which is the lower boundary for x values in the region. , which is the lower boundary for x values in the region.
On the other hand, the upper boundary for x values is  between 1 and between 1 and  ), and x=1 between ), and x=1 between  ) and ) and 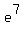 ). ).
So after all those calculations, we would end up with two integrals.
 , so , so
 = approx. 150.157 = approx. 150.157
|
|
|