Question 574988: Use the simplex method to maximize p= 5x+4y+3z subject to the constraints:
x>=0, y>=0, z>=0, x+y+z<=30, 2x+y+3z<=60, 3x +2y + 4z<= 84
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! Use the simplex method to maximize
P = 5x + 4y + 3z subject to the constraints:
x ≧ 0, y ≧ 0, z ≧ 0, x + y + z ≦ 30, 2x + y + 3z ≦ 60, 3x + 2y + 4z ≦ 84
You can ignore the three x ≧ 0, y ≧ 0, z ≧ 0, because the
process itself keeps the variables non-negative.
Put the constraint inequalities, first the objective
function equation ay the bottom{
x + y + z ≦ 30
2x + y + 3z ≦ 60
3x + 2y + 4z ≦ 84
p = 5x + 4y + 3z
Make the inequalities into equations by inserting
slack variables s1, s2 and s3
x + y + z + s1 = 30
2x + y + 3z + s2 = 60
3x + 2y + 4z + s3 - 84
p = 5x + 4y + 3z
Spread the slack variables out so that all variables are
lined up vertically, and and get zero on the right side
of the bottom equation by subtracting the right side from
both sides:
x + y + z + s1 = 30
2x + y + 3z + s2 = 60
3x + 2y + 4z + s3 = 84
-5x - 4y - 3z + P = 0
Put in 1 coefficients and 0 times the missing
variables,
1x + 1y + 2z + 1s1 + 0s2 + 0s3 + 0P = 30
2x + 1y + 3z + 0s1 + 1s2 + 0s3 + 0P = 60
3x + 2y + 4z + 0s1 + 0s2 + 1s3 + 0P = 84
-5x - 4y - 3z + 0s1 + 0s2 + 0s3 + 1P = 0
Make this into a matrix (tableau):
 Now we pivot, which involves five steps
1. finding the pivot element,
2. finding the pivot column,
3. finding the pivot row,
4. dividing the pivot row through by the element in the pivot row
5. using the resulting 1 in the pivot row to get 0's in all
the other positions in the pivot column.
1. The pivot element is the most negative element on the bottom row,
which is the -5 at the bottom of the 1st column.
2. The pivot column is the column containing the pivot element, which
is the 1st column.
3. The pivot row is found by dividing each positive number in the pivot
column into the number in the far right in its row.
Now we pivot, which involves five steps
1. finding the pivot element,
2. finding the pivot column,
3. finding the pivot row,
4. dividing the pivot row through by the element in the pivot row
5. using the resulting 1 in the pivot row to get 0's in all
the other positions in the pivot column.
1. The pivot element is the most negative element on the bottom row,
which is the -5 at the bottom of the 1st column.
2. The pivot column is the column containing the pivot element, which
is the 1st column.
3. The pivot row is found by dividing each positive number in the pivot
column into the number in the far right in its row.
 30÷1=30, 60÷2=30, 84÷3=28
The 28 is the smallest so so the 3rd row is the pivot row.
We divide the pivot row through by the 3
30÷1=30, 60÷2=30, 84÷3=28
The 28 is the smallest so so the 3rd row is the pivot row.
We divide the pivot row through by the 3
 Multiply row 3 by -1 and add to row 1
Multiply row 3 by -2 and add to row 2
Multiply row 3 by 5 and add to row 4
Multiply row 3 by -1 and add to row 1
Multiply row 3 by -2 and add to row 2
Multiply row 3 by 5 and add to row 4
 We repeat the process because there is still a negative number
on the bottom row.
1. The pivot element is the most negative element on the bottom row,
(in the case the only one) which is the
We repeat the process because there is still a negative number
on the bottom row.
1. The pivot element is the most negative element on the bottom row,
(in the case the only one) which is the 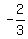 at the bottom of the 2nd
column.
2. The pivot column is the column containing the pivot element, which
is the 2nd column.
3. The pivot row is found by dividing each positive number in the pivot
column into the number in the far right in its row.
2÷ at the bottom of the 2nd
column.
2. The pivot column is the column containing the pivot element, which
is the 2nd column.
3. The pivot row is found by dividing each positive number in the pivot
column into the number in the far right in its row.
2÷ = 2· = 2·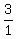 = 2·3 = 6
We skip dividing by the = 2·3 = 6
We skip dividing by the  , since it's negative:
28÷ , since it's negative:
28÷ = 28÷ = 28÷ = 42
The 6 is the smaller so the 1st row is the pivot row.
We divide the pivot row through by the = 42
The 6 is the smaller so the 1st row is the pivot row.
We divide the pivot row through by the  , which
is the same as multiplying it through by 3:: , which
is the same as multiplying it through by 3::
 Multiply row 1 by
Multiply row 1 by  and add to row 2
Multiply row 1 by and add to row 2
Multiply row 1 by 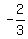 and add to row 3
Multiply row 1 by and add to row 3
Multiply row 1 by  and add to row 4 and add to row 4
 There are no more negative numbers on the bottom row, so
we are done pivoting.
Now we convert it back into a system of equations:
0x + 1y + 2z + 3s1 + 0s2 - 1s3 + 0P = 6
0x + 0y + 1z + 1s1 + 1s2 - 1s3 + 0P = 5
1x + 0y + 0z - 2s1 + 0s2 + 1s3 + 0P = 24
0x + 0y + 5z + 2s1 + 0s2 + 1s3 + 1P = 144
y + 2z + 3s1 - s3 = 6
z + s1 + s2 - s3 = 5
1x - 2s1 + s3 = 24
5z + 2s1 + s3 + P = 144
Solve the bottom equation for P:
P = 144 - 5z - 2s1 - s3
The most P can be is 144 and that is when z, s1 and s3 are all 0.
Substituting those:
y + 2(0) + 3(0) - (0) = 6
(0) + (0) + s2 - (0) = 5
x - 2(0) + (0) = 24
5(0) + 2(0) + (0) + P = 144
or
y = 6
s2 = 5
x = 24
P = 144
So P has maximum value 144 when x=24, y=6, and z=0
The slack variables turn out to be s1=0, s2=5, s3=0
Edwin
There are no more negative numbers on the bottom row, so
we are done pivoting.
Now we convert it back into a system of equations:
0x + 1y + 2z + 3s1 + 0s2 - 1s3 + 0P = 6
0x + 0y + 1z + 1s1 + 1s2 - 1s3 + 0P = 5
1x + 0y + 0z - 2s1 + 0s2 + 1s3 + 0P = 24
0x + 0y + 5z + 2s1 + 0s2 + 1s3 + 1P = 144
y + 2z + 3s1 - s3 = 6
z + s1 + s2 - s3 = 5
1x - 2s1 + s3 = 24
5z + 2s1 + s3 + P = 144
Solve the bottom equation for P:
P = 144 - 5z - 2s1 - s3
The most P can be is 144 and that is when z, s1 and s3 are all 0.
Substituting those:
y + 2(0) + 3(0) - (0) = 6
(0) + (0) + s2 - (0) = 5
x - 2(0) + (0) = 24
5(0) + 2(0) + (0) + P = 144
or
y = 6
s2 = 5
x = 24
P = 144
So P has maximum value 144 when x=24, y=6, and z=0
The slack variables turn out to be s1=0, s2=5, s3=0
Edwin
|
|
|