SOLUTION: Ok, so I just want to know the method of finding the base of a logarithm. I am given a picture of a graph; two points of a function, (3,5) and (5,9); and the asymptote: x=2 . I see

Algebra ->  Exponential-and-logarithmic-functions -> SOLUTION: Ok, so I just want to know the method of finding the base of a logarithm. I am given a picture of a graph; two points of a function, (3,5) and (5,9); and the asymptote: x=2 . I see      Log On


   

Question 574650: Ok, so I just want to know the method of finding the base of a logarithm. I am given a picture of a graph; two points of a function, (3,5) and (5,9); and the asymptote: x=2 . I see that there are 6 variables for me to find, and that I am given 5 numbers to "plug" in. I see how the graph points (3,5) and (5,9) fit into the equation y=alog↓b(x-h)+k, but I don't understand how to put the asymptote into the equation or how to find base b. Is there a specific way to find base b of a graph using these?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
You are trying to find a function where variable y depends on the value of variable x. What you need to find is values for a, b, h, and k. I would call a, b, h, and k parameters, because once we find them, they will be constants, while x and y will still be variables. Different values of those parameters will give different functions, but all those functions are part of the same family of functions.
You could say that y=log%2810%2Cx%29 is the mother of all the logarithmic functions. Or you could prefer to say that y=ln%28x%29 is the mother of them all. Or maybe you would like another base. Here are the graphs of y=log%281.6%2Cx%29 (red), and y=log%282%2Cx%29 (green):
graph%28200%2C200%2C-1%2C9%2C-5%2C5%2Clog%281.6%2Cx%29%2Clog%282%2Cx%29%29
The graph of y=a%2Alog%28b%2Cx%29 looks like that. No matter what values are chosen for a and b, the function only exists for x>0 and has x=0 for a vertical asymptote.
The graph of function y=a%2Alog%28b%2C%28x-h%29%29%2Bk is similar, but moved h units to the right and k units up. It only exists for x-h>0 (x>h) and its vertical asymptote would be x-h=0 or x=h. That's what happened to your function: h=2.
Now that you have y=a%2Alog%28b%2C%28x-2%29%29%2Bk, you can use the points given to find k (and a and b).
Point (3,5) says that 5=a%2Alog%28b%2C%283-2%29%29%2Bk --> 5=a%2Alog%28b%2C1%29%2Bk --> 5=a%2A0%2Bk --> 5=k
Now that you have y=a%2Alog%28b%2C%28x-2%29%29%2B5, you can use point (5,9) to find a and b.
9=a%2Alog%28b%2C%285-2%29%29%2B5 --> 9=a%2Alog%28b%2C3%29%2B5 --> 4=a%2Alog%28b%2C3%29 --> 4=a%281%2Flog%283%2Cb%29%29 --> a=4%2Alog%283%2Cb%29
That is all you can do. You could chose b=3, which would make a=4, and your solution would be
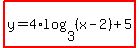
highlight%28y=4%2Alog%283%2C%28x-2%29%29%2B5%29
You could also chose b=9, which would make a=8, or infinite other choices. The function would be the same, just written in a different, equivalent form. It's just like 4/10 and 0.4 are different ways of writing 2/5, but it is still the same number.
Parameters a and b are related because the change of base is just a change of scale.