SOLUTION: The angles of triangle ABC are in the ratio of 8:3:4. What is the measure of the smallest angle?

Algebra ->  Triangles -> SOLUTION: The angles of triangle ABC are in the ratio of 8:3:4. What is the measure of the smallest angle?      Log On


   

Question 574560: The angles of triangle ABC are in the ratio of 8:3:4. What is the
measure of the smallest angle?
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
When you want to split a number N up into three parts 
in the ratio of P:Q:R, the three parts are:

1st part: 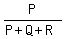P%2F%28P%2BQ%2BR%29·N
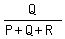2nd part: Q%2F%28P%2BQ%2BR%29·N
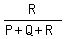3rd part: R%2F%28P%2BQ%2BR%29·N

You know that the sum of the three angles in any triangle
is 180°.

So you want to split N=180° up into three parts 
in the ratio of 8:3:4, so
P=8, Q=3, R=4

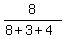1st part: 8%2F%288%2B3%2B4%29·180° = 8%2F15·180° = 96° 
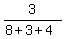2nd part: 3%2F%288%2B3%2B4%29·180° = 3%2F15·180° = 36°
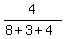3rd part: 4%2F%288%2B3%2B4%29·180° = 4%2F15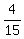·180° = 48°

The smallest of those three is 36°.

[As a check we add those three: 96°+36°+48°= 180°]

Edwin