Question 574517: what are the positive zeros of f(x)=2x^4-9x^3+2x^2+21x-10?
Found 2 solutions by Alan3354, KMST:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! what are the positive zeros of f(x)=2x^4-9x^3+2x^2+21x-10?
x = 1/2 & x = 2
--------------
Divide those out and solve the quadratic for the other 2, 1 is positive.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Rational zeros of a polynomial are fractions 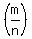 with only certain possible numbers for numerator and denominator. The numerator (m) must be a factor/divisor of the independent term (-10 in this case), so 1, 2, 5, and 10 are the only positive possibilities. The denominator (n) must be a factor of the leading coefficient of the polynomial (2 in this case), so 1, and 2 are the only positive possibilities. (The rational zero fractions can have a plus or minus sign, but we will look for only the positive ones). with only certain possible numbers for numerator and denominator. The numerator (m) must be a factor/divisor of the independent term (-10 in this case), so 1, 2, 5, and 10 are the only positive possibilities. The denominator (n) must be a factor of the leading coefficient of the polynomial (2 in this case), so 1, and 2 are the only positive possibilities. (The rational zero fractions can have a plus or minus sign, but we will look for only the positive ones).
Putting it all together, the only possible positive rational zeros are 1/2, 1, 2, 5/2, 5, and 10.



So far we have two positive zeros: 1/2 and 2.
That means the polynomial is divisible by 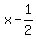 and by and by  . .
So it must be divisible by 
Dividing f(x) by 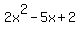 , I got , I got
 , so , so 
Solving  any which way we can (quadratic formula or completing the square), we get any remaining zeros of f(x). We get any which way we can (quadratic formula or completing the square), we get any remaining zeros of f(x). We get

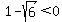 , so the positive zeros of f(x) are: , so the positive zeros of f(x) are:
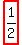 , ,  , and , and 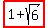 . .
|
|
|