Question 572524: Tom, dick, and harry paint houses. If all three work together, they finish in five days. If tom and dick work together they finish in eight days. If tom and harry work together they finish in ten days. How long would it take each one alone to paint a house?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Tom, dick, and harry paint houses.
If all three work together, they finish in five days.
If tom and dick work together they finish in eight days.
If tom and harry work together they finish in ten days.
How long would it take each one alone to paint a house?
:
Let t = Tom's time to paint the house alone
Let d = Dick's time
Let h = Harry's time
Let the competed job = 1
:
Write a shared work equation for each scenario
:
"Tom, dick, and harry paint houses. If all three work together, they finish in five days."
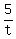 + + 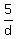 + + 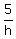 = 1 = 1
;
" If tom and dick work together they finish in eight days."
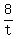 + + 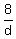 = 1 = 1
:
"If tom and harry work together they finish in ten days."
 + +  = 1 = 1
:
We can use elimination here, mult the 1st eq by 2, subtract the 3rd eq
 + + 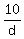 + +  = 2 = 2
 + + 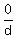 + +  = 1 = 1
-------------------------------------------subtraction eliminates t and h
10/d = 1
multiply both sides by d
d = 10 days for Dick to do the job alone
:
Use the 2nd equation to find t
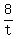 + + 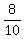 = 1; = 1;
multiply by 10t, results:
10(8) + t(8) = 10t
80 = 10t - 8t
80 = 2t
t = 40 days for Tom to do the job alone
:
Use the 3rd equation to find h
 + +  = 1 = 1
multiply by 40h
10h + 40(10) = 40h
400 = 40h - 10h
400 = 30h
h = 400/30
h = 13 days for Harry to do the job alone days for Harry to do the job alone
;
:
Let's see if this checks out using decimals in the 1st equation
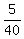 + +  + +  = 1 = 1
.125 + .50 + .375 = 1; confirms our solutions of:
:
Tom takes 40 days, rather useless
Dick takes 10 days, carrying the load
Harry takes 13 1/3 days, a good helper
|
|
|