Question 572471: Let X be a three digit number whose digits are all distinct. There are nine two-digit numbers that can be formed using the digits of X. Assume that X is the sum of all nine of these two digit numbers. Find all possible values of X.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! X cannot have zero for a digit.
If one of the digits of X was zero there would be only 2 choices for the tens digit when forming two-digit numbers. Then with 3 choices for the ones digit, there would be only 6 true two-digit numbers that could be made.
If the three digits of X are a, b, and c, each will appear 3 times as the tens digit and 3 times as the ones digit in the nine two-digit numbers.
The sum of the ones digits in the nine numbers will be
 and the sum of the tens digits will be the same.
The sum of the nine two-digit numbers will be
So  is a multiple of 3.
If a number is a multiple of 3, its digits must add to a multiple of 3.
Since is a multiple of 3, its digits must add to a multiple of 3.
So  for some integer 
Then, 
That means that is a multiple of 9.
If a number is a multiple of 9, its digits must add to a multiple of 9.
Since is a multiple of 9, its digits must add to a multiple of 9.
That means that 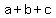 is a multiple of 9 too.
Since a, b, and c are different,
 and
The only choices are  and 
For ,  , but the digits of 297 add to 18, so it's not a solution.
For ,  , whose digits add up to 18.
|
|
|
