f(x) = -2(x-2)²(x+1)
To find the y-intercept substitute 0 for x
f(0) = -2(0-2)²(0+1)
f(0) = -2(-2)²(1)
f(0) = -2(4)
f(0) = -8
y-intercept (0,-8)
To find the x-intercept substitute 0 for f(x),
and remember that y and f(x) are the same thing.
f(x) = y = -2(x-2)²(x+1)
0 = -2(x-2)²(x+1)
Use the zero-factor property:
-2(x-2)² = 0 x+1 = 0
(x-2)² =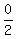 
x = -1
x-2=0 x-2=0
x=2 x=2
So the x-intercepts are (2,0) and (-1,0)
The x-value of the x-intercept 2 is a "double-zero"
since we got it twice. So the correct terminology is
"2 is a zero of multiplicity 2", which means
that the graph just touches the x-axis ("bounces off")
the x-axis, and does not cut through the x-axis.
The x-value of the x-intercept -1 is a "single-zero"
since we got it only once. So the correct terminology is
"2 is a zero of multiplicity 1", which means
that the graph cuts through the x-axis at that point.
We plot those intercepts, and use the fact that it cuts through the x-axis
at -1. It has to go down through (-1,0) to get to the y-intercept, (0,-8),
then it has to come back up to the x-axis and bounce off the x-axis at (2,0),
and then go back down.
Edwin
