Question 571610: . What is the largest natural number by which the product of three consecutive even natural numbers is Always divisible?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The smallest three consecutive even natural numbers are 2,4,and 6, and their product is 48, so the answer could be 48 or less, but cannot be more than 48 because that would not work for 2, 4, and 6.
For a general case, three consecutive even natural numbers can be represented as
  and and 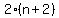
Their product would be

It is obviously divisible by 8, but there are factors in
  and and  that we have to take into account. that we have to take into account.
At least one of those three numbers is even (maybe just  ), so there is and factor 2 in ), so there is and factor 2 in 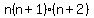 . .
At least one of   and and  is divisible by 3, so there is and extra factor 3 in is divisible by 3, so there is and extra factor 3 in 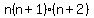 . .
We have the factors 8, 2, and 3, so the product of any three consecutive even natural numbers is always divisible by

|
|
|