Question 571203: In triangle ABC, a right triangle, the hypotenuse is 26 cm long. The altitude to the hypotenuse is 12 cm long. How long are the two segments of the hypotenuse formed by the altitude?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the altitude to the hypotenuse of a right triangle divides the right triangle into 3 similar triangles.
assume the altitude intersects the hypotenuse of triangle ABC at point D.
the 3 right triangles that are similar are:
ABC, ADB, CDB
since the triangles are similar, their corresponding angles are congruent and their corresponding sides are proportional.
if we label side AD equal to x and we label side CD equal to y, then we get a ratio of:
x/12 = 12/y
if we cross multiply, then we get:
xy = 12*12 which becomes:
xy = 144
since x + y = 26, we can solve for y to get:
y = 26 - x
we can substitute for y in the equation of:
xy = 144 to get:
x(26-x) = 144
simplify to get:
26x - x^2 = 144
add x^2 to both sides of this equation and subtract 26x from both sides of this equation to get:
x^2 - 26x + 144 = 0
this is a quadratic equation that factors to:
(x-8) * (x-18) = 0
this results in:
x = 8 or x = 18
if x = 8, then y = 18
if x = 18, then y = 8
this is because y = 26 - x.
we will allow x to be equal to 8 which results in y being equal to 18.
those are the 2 segments of the hypotenuse formed by the altitude.
the following diagram should help display what is happening.
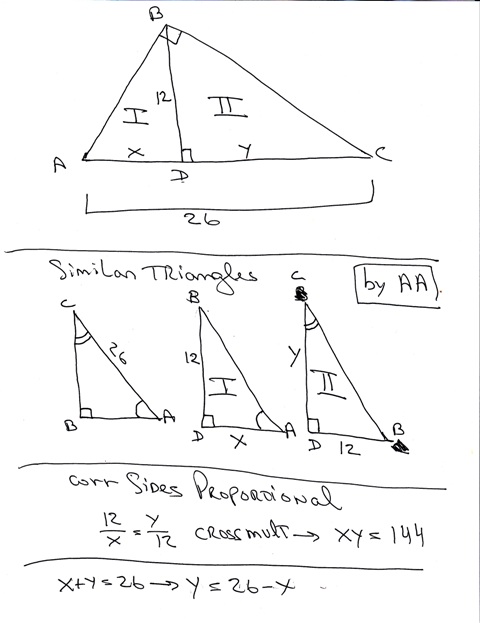
this is what is called the mean proportional in a right triangle.
a tutorial that discusses that can be found here:
http://www.regentsprep.org/Regents/math/geometry/GP12/LMeanP.htm
|
|
|