SOLUTION: Suppose a genius figured out that sin(7pi/12)= -((sqrt(2)+sqrt(60)/4) Find each of the following exactly (show steps) a). sin (-(7pi/12)) b.) sin (-(5pi/12)) c. cos

Algebra ->  Trigonometry-basics -> SOLUTION: Suppose a genius figured out that sin(7pi/12)= -((sqrt(2)+sqrt(60)/4) Find each of the following exactly (show steps) a). sin (-(7pi/12)) b.) sin (-(5pi/12)) c. cos      Log On


   

Question 570994: Suppose a genius figured out that
sin(7pi/12)= -((sqrt(2)+sqrt(60)/4)
Find each of the following exactly (show steps)
a). sin (-(7pi/12))
b.) sin (-(5pi/12))
c. cos(pi/12)
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
It does not take a genius to find the exact value of 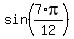sin%287%2Api%2F12%29, but having those trigonometric identity formulas handy helps.
The expression you posted for 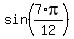sin%287%2Api%2F12%29 is wrong. Either someone made a typo somewhere, or the person who wrote the problem is trying to confuse us all.
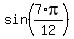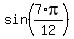Since the expression given for sin%287%2Api%2F12%29 looked fishy to me, I went looking for the trigonometric identity formulas to find the correct exact value of sin%287%2Api%2F12%29.
It turns out that highlight%28sin%287%2Api%2F12%29=%28sqrt%282%29%2Bsqrt%286%29%29%2F2%29%29
HOW I CALCULATED THAT (just in case you care)
I found the trigonometric identity
sin%28A%2BB%29=sin%28A%29cos%28B%29%2Bcos%28A%29sin%28B%29
and that was useful, because I know that
1%2F4%2B1%2F3=3%2F12%2B4%2F12=7%2F12 so pi%2F4%2Bpi%2F3=7pi%2F12
and everybody knows that
sin%28pi%2F4%29=cos%28pi%2F4%29=sqrt%282%29%2F2
sin%28pi%2F3%29=sqrt%283%29%2F2 and
cos%28pi%2F3%29=1%2F2
So
=

BACK TO THE PROBLEM
I am going to use highlight%28sin%287%2Api%2F12%29=%28sqrt%282%29%2Bsqrt%286%29%29%2F2%29%29
However, it turns out that all the answers are either that expression, or (-1) times that, so if you were meant to use the fishy expression, you'll easily figure out the intended answers
a) sin%28-anything%29=-sin%28anything%29 so

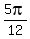b) 5pi%2F12%2B7pi%2F12=12pi%2F12=pi so 5pi%2F12 and 7pi%2F12 are supplementary angles. They add up to pi, which is 180%5Eo.
And we know that 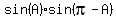sin%28A%29sin%28pi-A%29
so sin%285pi%2F12%29=sin%287pi%2F12%29=%28sqrt%282%29%2Bsqrt%286%29%29%2F2%29
and
c) pi%2F12=7pi%2F12-6pi%2F12=7pi%2F12-pi%2F2
I think we are expected to go to that table of trigonometric identities to find
cos+%28A-B%29=cos%28A%29cos%28B%29%2Bsin%28A%29sin%28B%29
Luckily, as everybody knows, cos%28pi%2F2%29=0 and sin%28pi%2F2%29=1
So