SOLUTION: Find a 4th degree polynomial equation with integer coefficients which has two irrational roots, one of which is 2+3{{{sqrt(5)}}}, and two imaginary roots, one of which is 3-2i.

Find a 4th degree polynomial equation with integer coefficients which has 
two irrational roots, one of which is 2+3, and two imaginary
roots, one of which is 3-2i.

In order to have integer coefficients if a polynomial equation has
the irrational root 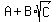, it must also have its conjugate
.  Similarly if it has an imaginary root C+Di as a root,
it must also have its conjugate C-Di as a solution. 

So, since it must have integer coefficients, and 2+3 is a root,
then 2-3 is also a root.  And since it has 3-2i as a root,
3+2i is also a root.  So if it were solved we would have to end up with
these four solutions:

x = 2+3, x = 2-3, x = 3-2i, x = 3+2i

So before that we would have had

x - (2+3) = 0, x - (2-3) = 0, x - (3-2i) = 0, x - (3+2i) = 0

And before that we would have had:

x - 2 - 3 = 0, x - 2 + 3 = 0, x - 3 + 2i = 0, x - 3 - 2i = 0

And before that we would have had:

(x - 2 - 3)(x - 2 + 3)(x - 3 + 2i)(x - 3 - 2i) = 0

Now we must multiply that out and collect terms to get our fourth
degree polynomial equation:

It will be easier if we group the first two terms in each parentheses:

[(x-2) - 3][(x-2) + 3][(x-3) + 2i][(x-3) - 2i] = 0

The first two bracket expressions are like multiplying (A+B)(A-B)=A²-B², and
the last two bracketed expressions are too:

[(x-2)² - 9·5][(x-3)² - 4i²] = 0

[(x-2)² - 45][(x-3)² - 4(-1)] = 0

[(x-2)² - 45][(x-3)² + 4] = 0

[x²-4x+4 - 45][x²-6x+9 + 4] = 0

(x² - 4x - 41)(x² - 6x + 13) = 0

x4 - 6x³ + 13x² - 4x³ + 24x² - 52x - 41x² + 246x - 533 = 0

x4 - 10x³ - 4x² + 194x - 533 = 0

Edwin