|
Question 570370: Using the Gauss/Jordan method to solve the system, writing all row operations between the affected matrices, using the format: rn + k x rm = Rn The system is: x-2y+z=6
2x+y-3z=-3
x-3y+3z=10
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!


 We want to try to end up with a matrix
that looks like this:
We want to try to end up with a matrix
that looks like this:
 with 0's in the three lower left hand positions:
We can get a 0 where the 2 is by multiplying Row 1 by -2
and adding it to row 2:
That instruction is written as
-2ĚR1+1ĚR2->R2
with 0's in the three lower left hand positions:
We can get a 0 where the 2 is by multiplying Row 1 by -2
and adding it to row 2:
That instruction is written as
-2ĚR1+1ĚR2->R2
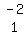 
 Notice that Row 2 will be simpler if we divide it through by 5,
That instruction is written
Notice that Row 2 will be simpler if we divide it through by 5,
That instruction is written  R2->R2 R2->R2
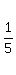 
 We can get a 0 where the 1 is in the lower left corner by
multiplying Row 1 by -1 and adding it to row 3:
That instruction is written as
-1ĚR1+1ĚR3->R3
We can get a 0 where the 1 is in the lower left corner by
multiplying Row 1 by -1 and adding it to row 3:
That instruction is written as
-1ĚR1+1ĚR3->R3
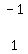 
 We can get a 0 where the -1 is in the bottom row by
multiplying Row 2 by 1 and adding it to row 3:
That instruction is written as 1R2+1R3->R3
We can get a 0 where the -1 is in the bottom row by
multiplying Row 2 by 1 and adding it to row 3:
That instruction is written as 1R2+1R3->R3
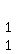 
 Now that we have 0's in the lower lefthand corner,
we convert the matrix back to a system of equations
in x, y and z:
Now that we have 0's in the lower lefthand corner,
we convert the matrix back to a system of equations
in x, y and z:
 or just
or just
 Now we use back substitution.
From the third equation, z=1, we substitute
that into the middle equation, getting:
y-z = -3
y-1 = -3
y = -2
Then substitute y=-2 and z=1 in the 1st equation:
x-2(-2)+(1) = 6
x+4+1 = 6
x+5 = 6
x = 1
Solution (x,y,z) = (1,-2,1)
Edwin
Now we use back substitution.
From the third equation, z=1, we substitute
that into the middle equation, getting:
y-z = -3
y-1 = -3
y = -2
Then substitute y=-2 and z=1 in the 1st equation:
x-2(-2)+(1) = 6
x+4+1 = 6
x+5 = 6
x = 1
Solution (x,y,z) = (1,-2,1)
Edwin
|
|
|
| |