Question 569553: Peter works as an electrical engineer for an electrical firm,His total salary for his first year of work at this firm is $60,000.peter's annual salary increases by 10% of his first year's salary,Find
I)His total salary after 10 years
II) the least value of 'n' fir which his total salary after 'n' years is more than 2milion dollars
b) John is an electrical engineer in a rival firm,His total salary for the first year is also $60,000.But his annual salary follows a geometric progession.If he earns $75,600 in his 4th year of work,find
i)his annual percentage increase in salary,
II) his total salary after 10 years
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I believe they mean that poor Peter, gets a raise of (0.10)($60,000)= $6,000 every year. His salary goes up in an arithmetic sequence (or arithmetic progression).
In the 10th year, after 9 raises, he gets $60,000+9($6,000)=$60,000+$54,000=$114,000.
The sum of an arithmetic progression is the average of first and last terms, multiplied times the number of terms.
I) Adding up Peterís 10 years of salary we get 10($60,000+$114,000)/2=$870,000. I believe Thatís what the problem means by ďHis total salary after 10 years.Ē
II) Another way to calculate the sum  of the first of the first  terms of an arithmetic progression starting with terms of an arithmetic progression starting with  and increasing by and increasing by  from term to term is from term to term is

In Peterís case,  and and  , so , so

To find out when  we solve we solve
 ---> --->  --> --> 
 using the quadratic formula. We simplify to using the quadratic formula. We simplify to
 , which rounds to 18.01 , which rounds to 18.01
That means that 18 years is not quite enough. In fact

Peter will have collected $2,000,000 in salary at some point during his 19th year, and after 19 years he will have totaled $2,166,000 in earnings, so I suspect the answer expected for part II) is 19.

b)Johnís annual salary follows a geometric progression starting at $60,000, and earns $75,600 in his 4th year of work.
I) Letís find his annual percentage increase in salary,
In a geometric sequence (or geometric progression), each term is the product of the term before times a common ratio, r. After raises at the end of the first 3 years, Johnís salary for the fourth year is
$60,000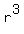 =$75,000, so =$75,000, so 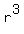 =$75,000/$60,000=5/4=1.25 and =$75,000/$60,000=5/4=1.25 and
 = 1.0772 (rounded) = 1.0772 (rounded)
Each year end he gets a raise worth 0.0772 times the prior year salary, or  % of the prior year salary. % of the prior year salary.
John may look at Peter in envy at the end of the first year, but his raise is always 7.72% of the latest salary, and keeps growing, while Peterís raises are always the same $6,000 (10% of his starting salary). Peter had a salary of $60,000+3($6,000) =$78,000 for the fourth year, but soon John overtakes Peter in salary
II) Letís find Johnís total salary after 10 years
For the 10th year, Johnís annual salary should be $60,000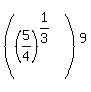 =$60,000 =$60,000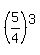 =$117,187.50 (already ahead of Peter) =$117,187.50 (already ahead of Peter)
However, he is not yet ahead in terms of total earnings.
The sum of n terms of a geometric progression of common ratio  , starting with , starting with  is calculated as is calculated as
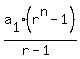
In this case $60,000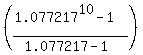 = $60,000 = $60,000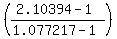 = $60,000 = $60,000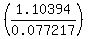 = $857,791.83 (rounded) = $857,791.83 (rounded)
|
|
|