Question 566374: You have saved a total of more than $75 but less than $120. When you count your money, you find that you have some one dollar bills, some five, and some tens. You have twice as many tens as fives and four times as many ones than fives. How much money could you have? Write equations and/or inequalities (using "t" for ttens, "f" for fives and "n" for ones) in order to solve. Explain your work.
I know I have to start with 2t than 5 + 4x than ones. Now I am stuck.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let  be the number of $1 bills; be the number of $1 bills;
let  be the number of $5 bills, and be the number of $5 bills, and
Let  be the number of $10 bills, as suggested be the number of $10 bills, as suggested
We start with equations, because some numbers seem to be equal.
We can translate "twice as many tens as fives" as

We can translate "four times as many ones than fives" as
 , although I would have stated that as "four times as many ones as fives." , although I would have stated that as "four times as many ones as fives."
The total amount of money would be $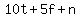 , but we can substitute the expressions above to have everything as a function of , but we can substitute the expressions above to have everything as a function of  , the number of $5 bills. , the number of $5 bills.
$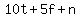 =$ =$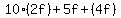 =$ =$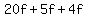 =$ =$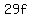
So we have $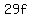 . .
We know that the amount is "more than $75 but less than $120," so
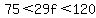 <--- That's two inequalities in one, but it's OK to write it like this (at least in my book). <--- That's two inequalities in one, but it's OK to write it like this (at least in my book).
So we divide all 3 sides of the inequalities by 29 and get an equivalent double inequality.
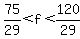
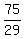 is approximately 2.586 and is approximately 2.586 and 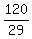 is approximately 4.138, but is approximately 4.138, but  is suposed to be a natural number (a positive integer). is suposed to be a natural number (a positive integer).
So it could only be  , or , or  . .
If  , the amount of money you have is $ , the amount of money you have is $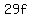 =$ =$ =$87. =$87.
If  , the amount of money you have is $ , the amount of money you have is $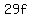 =$ =$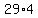 =$116. =$116.
|
|
|