[Notice that I changed your letter "x" to the letter "a" because this problem
is about an unknown constant, but "x" is a variable. The problem would be
very confusing if we let "x" be both an unknown constant and a variable as well.
If this problem was given with "x" representing an unknown constant,
you should point this out to your teacher.]
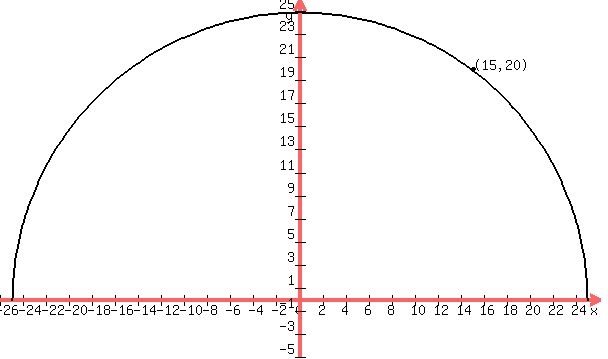
A semicircle has a radius of a + 5 and the center is the origin. The point (15, a) lies on the circle. Solve for a.
x² + y² = r²
x² + y² = (a + 5)²
Substitute in the point (15, a)
15² + a² = (a + 5)²
225 + a² = (a + 5)(a + 5)
225 + a² = a² + 10a + 25
200 = 10a
20 = a
So the radius is a + 5 or 20 + 5 or 25, and the point (15,a) is (15,20).
and the grpah is this:
 Edwin
Edwin