Question 564909: Hey! Im currently in e2020 and im a visual learner NOT a person who learns just by hearing, but im in need of someone to help me on this math problem:
finding the vertex of y=x^2+3x-4
Found 2 solutions by Alan3354, lwsshak3:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! finding the vertex of y=x^2+3x-4
--------
The vertex is on the LOS, the Line of Symmetry.
The LOS is x = -b/2a = -3/2
x = -3/2
-------
The vertex is (-3/2,f(-3/2))
f(-3/2) = (-3/2)^2 + 3*(-3/2) - 4 = 9/4 - 18/4 - 16/4
= -25/4
-------
Vertex at (-3/2,-25/4)
or (-1.5,-6.25)
======================
You can find it by putting the eqn in standard form, also.
y=x^2+3x-4 = (x^2 + 3x + 2.25) - 4 - 2.25
y = (x + 1.5)^2 - 6.25
--> vertex at (-1.5,-6.25)
Answer by lwsshak3(11628)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hey! Im currently in e2020 and im a visual learner NOT a person who learns just by hearing, but im in need of someone to help me on this math problem:
finding the vertex of y=x^2+3x-4
**
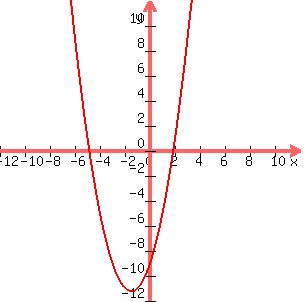
Since this is a 2nd degree equation you should know that its graph is a parabola.
The standard form of this equation: y=A(x-h)^2+k, (h,k) being the (x,y) coordinates of the vertex. A is a multiplier which affects the slope or steepness of the curve.
..
To rewrite equation in standard form, complete the square:
y=(x^2+3x+9/4)-4-9/4
y=(x+3/2)^2-45/4
This is an equation of a parabola with vertex at (-3/2,-45/4).
Since the lead coefficient>0, parabola opens upwards
see graph below as a visual check:
|
|
|