Question 563136: Hi --
I'm a beginning student in Linear Algebra, and am not quite sure how to answer the following question, which is taken from my textbook:
"Suppose the system below is consistent for all possible values of f and g. What can you say about the coefficients c and d. Justify your answer.
2x + 4y = f
cx + dy = g."
Not quite sure what is meant by the question "what can you say." My only thought so far is that If the system is consistent, that means x and y have the same value for both equations:
x(2 + c) + y(4 + d) = f + g, which, if c = f+g, fits into the form ax + by = c. But that's about it.
Thanks in advance!
Cheers,
Dave Yrueta
Answer by Edwin McCravy(20064)   (Show Source):
You can put this solution on YOUR website!
No, they are consistent if they have a solution.
So we find what their solution must be by elimination:
2x + 4y = f
cx + dy = g
Multiply the first equation through by -d and the
second equation through by 4
-2dx - 4dy = -df
4cx + 4dy = 4g
(4c-2d)x = 4g-df
x =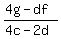 
Start over:
2x + 4y = f
cx + dy = g
Multiply the first equation through by c and the second equation through
by -2
2cx + 4cy = cf
-2cx - 2cy = -2g
(4c-2d)y = cf-26
y = 
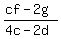Notice that for both x and y, the denominators
are the same, 4c-2d
In order for those expresions for x and y to be
defined solution, their denominators must not be
zero, because division by 0 is not defined. But
division by any other number is defined. Therefore
the only requirement is that their denominator must
not be equal to 0, so
4c-2d ≠ 0
divide through by 2
2c-d ≠ 0
2c ≠ d
d ≠ 2c
As long as d is not equal to 2c, there will be a solution for
any values of f and g.
The answer to: "What can you say about the coefficients c and d?" is
d is not equal to 2c.
[If you have studied Cramer's rule, you can just say the determinant of
coefficients D must not equal 0. The above was done assuming you have not
studied or were not allowed to use Cramer's rule.]
Edwin
|
|
|
