SOLUTION: Here it is again! I know how to do this, I just don't have the resourse, can someone help me to graph this problem x-y<3 x+2y>6 another problem that I have is, solve the syste

Here it is again! I know how to do his,I just don't have the 
resourse, can someone help me to graph this problem.

x -  y < 3
x + 2y > 6

This is the graph of a shaded region


First draw the graphs of the boundary lines.  

Boundary line's equations:  |  Boundary line's intercepts
                            | 
       x -  y = 3           |    (0,-3)         (3,0)   
       x + 2y = 6           |     (0,3)         (6,0) 
                            |
---------------------------------------------------------

Just draw one boundary line at a time so you can tell
which area to shade.

Draw the first bondary line by plotting its two intercepts
and drawing a dotted line thru them.  Draw it dotted since
it is strictly less than.  I can only draw it solid on here,
but you can draw it dotted on your paper:



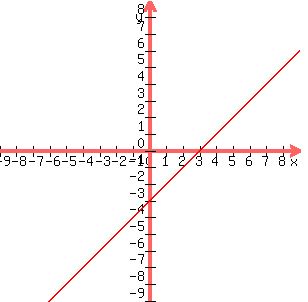Now before drawing the other boundary line, we must decide which
side of this line we will shad on.

To do this we pick any point which is not on that line as a test
point, say, we pick (3,2) for we can be sure that is not on the
line.  We substitute x=3 and y=2 into the inequality

x - y < 3
3 - 2 < 3
    1 < 3

That is a true inequality, since 1 really is less than 3, so we 
know to shade the side of the boundary line that the test point 
(3,2) is on.  That's the side above the line. [BTW if that
inequality had come out false, then we'd have known to shade the
other side, the lower side. instead.]

Now draw the second boundary line by plotting its two intercepts
and drawing a dotted line thru them.  Draw it dotted also since
it is strictly greater than.  I can only draw it solid on here,
but you can draw it dotted on your paper:



Now we must also decide which side of this line we will shade.

As before, to do this we pick any point which is not on that line 
as a test point, say, we pick (2,1) for we can be sure that is not 
on the green line.  We substitute x=2 and y=1 into the inequality

  x + 2y > 6
2 + 2(1) > 5
       4 > 5

That is a false inequality, since 4 is NOT greater than 5, so we 
know to shade the side of the boundary line that the test point 
(2,1) is NOT on.  That's the side above the green line.    
 
So the section we shade is the V-shaped region which is above
both the red and the green lines.  And the lines are supposed
to be drawn dotten, not solid.  [You would have drawn them
solid if the inequalities had been < or >.]

==============================================================


another problem that I have is, solve the system by addition or 
substitution.

3x + 6y = 0
      x = 2/3 

Since the second equation already gives you the value for x,
namely 2/3, the problem is half-worked for you from the start.

So all you have to do is finish by substituting 2/3 for x in 
the first equation and solve for y.

    3x + 6y = 0
3(2/3) + 6y = 0     
     2 + 6y = 0
         6y = -2
          y = -2/6
          y = -1/3

So the solution is (x,y) = (2/3,-1/3)

Edwin