|
Question 561896: What number is the sum of 17 times its first digit, 34 times its second digit, and 51 times its third digit? Why?
Found 2 solutions by ankor@dixie-net.com, richard1234:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! What number is the sum of 17 times its first digit, 34 times its second digit, and 51 times its third digit? Why?
:
Let a = the 100's (1st digit)
Let b = the 10's (2nd digit)
Let c = the unit (3rd digit)
:
100a + 10b + c = 17a + 34b + 51c
100a - 17a = 34b - 10b + 51c - c
83a = 24b + 50c
a = 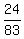 b + b + 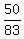 c c
Tried various values for c, only c=9, gave integer values for a and b
Used the table on a ti83 with this equation entered
:
a=6, b=2
:
629 is the number
;
:
Check:
17(6) + 34(2) + 51(9) =
102 + 68 + 459 = 629
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! If a,b,c denote the digits, then
 (right away we know the number is a multiple of 17) (right away we know the number is a multiple of 17)

Here, we conclude that a is even (since RHS is even). Now consider the equation mod 10 (if you don't know modular arithmetic, think of it as "matching the units digits on LHS and RHS").
If a = 2, then b = 4 or 9, but neither allows for an integer value of c. If a = 4, then b = 3 or 8, but likewise, there are no integer solutions for c. If a = 6, then b = 2 or 7, and it can be checked that b = 2 allows for the number 629. If a = 8, then b = 1 or 6, but neither allows for integer solutions.
Hence the only number is 629.
|
|
|
| |