Question 560284: A common ant absorbs oxygen at a rate of about 6.2 mililiters per second per square centimeter of exoskeleton. It needs about 24 mililiters of oxygen per second per cubic centimeter of its body. An ant is basically cylindrical in shape, so its surface area S and volume V can be approximated by the formulas for the surface area and volume of a cylinder:
S=2πh+2πr^2
V=πr^2h
a) Approximate the surface area and volume of an ant that is 8 mm long and has a radius of 1.5 mm. would this ant have a surface area large enough to meet its oxygen needs?
b) Consider a "giant" ant that is 8m long and has a radius of 1.5m. would this ant have a surface area large enough to meet its oxygen needs?
c) substitute 1000r for r and 1000h for h into the formulas for surface area and volume. how does increasing the radius by height by a factor of 1000 effect surface area> How does it affect volume? Use the results to explain why "giant" ants do not exist.
Found 2 solutions by Theo, KMST:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! surface area of ant is given by equation for surface area of a cylinder which is:
S = 2 * pi * r^2 + 2 * pi * r * h
you were missing an "r" in the surface area formula.
i provided the correction for you.
-----
before you start, you should convert everything to common measure.
that common measure has been chosen to be centimeters since the oxygen absorption rate and the oxygen requirement rate is in centimeters.
-----
mm = millimeters
cm = centimeters
m = meters
ml = milliliters
-----
the conversion rate for mm to cm is that 1 cm = .1 mm.
the conversion rate for m to cm is that 1 cm = 100 m.
this means that:
you multiply your mm by .1 to get the equivalent number of cm.
you multiply your m by 100 to get the equivalent number of cm.
-----
the conversion calculator used is at this link:
http://www.onlineconversion.com/length_common.htm
-----
based on these conversion rate, our measurements can be translated as follows:
a normal ant measures 8mm in length which is equivalent to .8cm.
a giant ant measure 8m in length which is equivalent to 800cm.
the radius of a normal ant is equal to 1.5mm which is equivalent to .15cm.
the radius of a giant ant is equal to 1.5m which is equivalent to 150cm.
-----
your measurements becomes:
length of normal ant is .8cm.
radius of normal ant is .15cm.
length of giant ant is 800cm.
radius of giant ant is 150cm.
-----
you can now tackle this problem using the common measure of cm.
-----
the formula for the surface area of ant is equal to:
S = 2*pi*r*h + 2*pi*r^2
for the normal ant, this becomes:
Sn = 2*pi*.15*.8 + 2*pi*.15^2 which becomes:
Sn = .24*pi + .045*pi which becomes:
Sn = .285*pi square cm *****
for the giant ant, this becomes:
Sg = 2*pi*150*800 + 2*pi*150^2 which becomes:
Sg = 240,000*pi + 45,000*pi which becomes:
Sg - 285,000*pi square cm *****
-----
the formula for the volume of an ant is equal to:
V = pi*r^2*h
for the normal ant, this becomes:
Vn = pi*.15^2*.8 which becomes:
Vn = .018 cubic cm *****
for the giant ant, this becomes:
Vg = pi*150^2*800 which becomes:
Vg = 18,000,000 cubic cm *****
-----
your measurements are:
normal ant:
surface area = .285 * pi square cm.
volume = .018 * pi cubic cm.
giant ant:
surface area = 285,000 * pi square cm.
volume = 18,000,000 * pi cubic cm.
-----
oxygen absorption rate for an ant is equal to 6.2 milliliters per second for every square centimeter of surface area.
the normal ant is therefore absorbing:
6.2 * .285 * pi = 1.767 * pi milliliters of oxygen per second.
the giant ant is therefore absorbing:
6.2 * 285,000 * pi = 1,767,000 * pi milliliters of oxygen per second.
-----
oxygen requirement rate for an ant is equal to 24 milliliters per second for every cubic centimeter of volume.
the normal ant therefore requires:
24 * .018 * pi = .432 * pi milliliters of oxygen per second.
the giant ant therefore requires:
24 * 18,000,000 * pi = 432,000,000 * pi milliliters of oxygen per second.
-----
the normal ant absorbs 1.767 * pi milliliters of oxygen per second and requires .423 * pi milliliters of oxygen per second so the normal ant gets plenty of oxygen to survive.
-----
the giant ant absorbs 1,767,000* pi milliliters of oxygen per second and requires 432,000,000 * pi milliliters of oxygen per second so there is no way the giant ant could survive since the requirement rate far exceed the absorption rate.
-----
if you look at the formulas involved, you see that:
S = 2*pi*r*h + 2*pi*r^2
V = pi * r^2 * h
if you multiply r by 1000 and h by 1000, then the surface area becomes:
S = 2*pi*r*h*1,000,000) + 2*pi*r^2*1,000,000 which becomes:
S = 1,000,000 * (2*pi*r*h + 2*pi*r^2) which basically multiplies the surface area by a million.
if you multiply r by 1000 and h by 1000, then the volume formula becomes:
V = pi * (1,000,000) * r^2 * 1000 * h which become:
V = (1,000,000,000) * pi * r^2 * h which basically multiplies the volume by a billion.
since the surface area is multiplied by 1 million times and the volume area is multiplied by 1 billion times then you can see that:
the normal ant absorbing 1.767 * pi milliliters of oxygen per second will absorb 1 million times that to absorb 1,767,000 * pi milliliters of oxygen per second.
the normal ant requiring .423 milliliters of oxygen per second will require 1 billion times that to require 423,000,000 * pi milliliters per second.
-----
the ratio of absortion rate per second to requirement rate per second for the normal ant is:
1.767 divided by .432 which equals 3.99537037
the normal ant is absorbing oxygen at a rate of 3.99537037 times the rate that it requires so the ant is able to survice.
multiply the absorption rate by 1 million and the requirement rate by 1 billion and the ratio becomes:
1.767 * 1 million divided by .432 * 1 billion which becomes:
1.767 divided by .423 * 1 billion which becomes:
1.767 divided by 423 which equals .004177305
the giant ant is absorbing oxygen at a rate of .004177305 times the rate that it requires so the ant is not able to survive.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The formula to calculate surface area of a cylinder is  (You had a typo). (You had a typo).
The formula to calculate its volume is 
Using the measurements in cm, square centimeters (sq cm), and cubic centimeters (cc) would be best.
1 mm = 0.1 cm, so 8 mm = 0.8 cm and 1.5 mm = 0.15 cm (you just divide by 10)
1 m = 100 cm, so 8 m = 800 cm and 1.5 m = 150 cm (you just multiply times 100)
Your teacher probably expects you to use the approximation  =3.14, so I'll use that. =3.14, so I'll use that.
a) For a cylindrical ant that is 8 mm long and has a radius of 1.5 mm:
S = 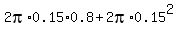 = approx. 0.89 sq cm = approx. 0.89 sq cm
V = 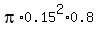  = approx. 0.057 cc = approx. 0.057 cc
In one second, it would absorb 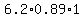 mL oxygen = 5.5 mL oxygen. mL oxygen = 5.5 mL oxygen.
During that second it would require 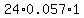 mL oxygen = 1.37 mL oxygen. mL oxygen = 1.37 mL oxygen.
This ant would have a surface area large enough to meet its oxygen needs.
b) For a "giant" ant that is 8m long and has a radius of 1.5m (1,000 times longer in every direction):
S = 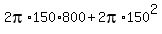 = 890,000 sq cm = = 890,000 sq cm = 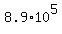 sq cm sq cm
V = 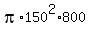  = approx. 57,000,000 cc = = approx. 57,000,000 cc = 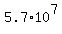 cc cc
In one second, it would absorb 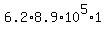 mL oxygen = 5,500,000 mL oxygen = mL oxygen = 5,500,000 mL oxygen = 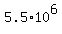 mL oxygen. mL oxygen.
During that second it would require 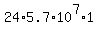 mL oxygen = 1,370,000,000 mL oxygen = mL oxygen = 1,370,000,000 mL oxygen = 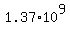 mL oxygen. mL oxygen.
This ant would not have a surface area large enough to meet its oxygen needs.
c) Substituting 1000r for r and 1000h for h into the formulas for surface area and volume, we see that
S = 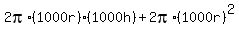 = = 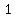 and and
V = 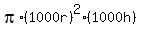 = = 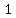
With the same shape, as the length measurements increase by a factor of 1,000, the surface are increases by a factor of 1,000,000 (1,000^2), and the volume increases by a factor of 1,000,000,000 (1,000^3).
NOTE: The same is true for any shape (not just cylinders), and any factor (not just 1,000).
|
|
|