Question 559518: If  and and  . Express . Express 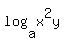 in terms of P and 7. in terms of P and 7.
 => => 
 => => 
Log(a,(a^P)^2a^7 ) => Log( a, a^2Pa^7 )
and I was stuck. I am not even sure of what i'm doing ????
So, please help.
Found 3 solutions by KMST, htmentor, Theo:
Answer by KMST(5328)   (Show Source): (Show Source):
Answer by htmentor(1343)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your problem states:
log(a,x) = p
log(a,y) = 7
you want to express log(a,x^2*y) in terms of p and 7.
start with log(a,x^2*y)
this becomes:
log(a,x^2) + log(a,y) which becomes:
2*log(a,x) + log(a,y)
since log(a,x) = p and log(a,y) = 7, your equation becomes:
2*p + 7
it can also be shown as:
2p + 7
the logarithm rules you are using are:
log(x*y) = log(x) + log(y)
log(x^y) = y*log(x)
these rules apply regardless of the base of the logarithm that is being used.
|
|
|