Question 559457: The Greek God Zeus ordered his blacksmith Hephaestus to create a perpetual water-making machine to fill Zeus' mighty chalice. The volume of Zeus' chalice was reported to hold about One hundred and fifty sextillion gallons (that is a fifteen followed by twenty-two zeros). If Hephaetus' machine pours out 2 gallon in the first minute and then doubles its output each minute, find in
which minute would this hypothetical machine pour out a single quantity of water that would be enough to fill Zeus' chalice with water?
put in minutes
i only get the 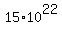 I dont know how to set this problem up to solve as my logrithmic knowledge is minor
Help will be greatly appreciated
Found 2 solutions by ankor@dixie-net.com, htmentor:
Answer by ankor@dixie-net.com(22740)   (Show Source):
Answer by htmentor(1343)  (Show Source):
You can put this solution on YOUR website! The Greek God Zeus ordered his blacksmith Hephaestus to create a perpetual water-making machine to fill Zeus' mighty chalice. The volume of Zeus' chalice was reported to hold about One hundred and fifty sextillion gallons (that is a fifteen followed by twenty-two zeros). If Hephaetus' machine pours out 2 gallon in the first minute and then doubles its output each minute, find in
which minute would this hypothetical machine pour out a single quantity of water that would be enough to fill Zeus' chalice with water?
============================================================
First, consider how much water is added to the chalice each minute.
During the 1st minute, there are 2 gallons added to the chalice
During the 2nd minute, there are 4 gallons added
During the 3rd minute, there are 8 gallons added, etc.
The number of gallons added for each successive minute consists of a geometric sequence: 2,4,8,16,...
To determine how long it takes to fill the chalice, we need to sum this sequence
The sum of a geometric sequence with common ratio r is:
S(n) = a(1-r^n)/(1-r) where a = the first term
In this case a = 2 and r = 2:
S(n) = 2(1-2^n)/(1-2) = 2(2^n - 1) = 15*10^22
We need to solve for n:
2^n - 1 = 7.5E22 [Scientific notation]
2^n = 7.5E22 + 1
Take the logarithm of both sides:
n*log(2) = log(7.5E22 + 1)
n = 22.875/0.301 = 75.997 min., so the chalice gets filled in the 76th minute
|
|
|
