Question 559431: A triangle has side lengths measuring 4 and 5. The measurement of the smallest side is missing. Ted says one possibility for the unknown side length is 3. Do you agree with Ted? Explain why or why not.
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! You should agree with Ted.
.
You need to be sure that Ted has actually proposed dimensions that will form a triangle. You do this by ensuring that when you add the two shorter sides together, that sum is longer than the longest side. If this is not true, then a triangle cannot be formed. (The reason for this is discussed in the last paragraph below.) In Ted's proposal the two shorter sides are 3 and 4. The sum of these two lengths is 7 and since that sum is greater than the longest side, 5, then Ted's proposed sides can form a triangle. This is enough to prove that Ted is correct.
.
As further information, and this comes from experience, the sides that Ted has proposed will form a right triangle. You can demonstrate this by using the Pythagorean theorem. This theorem states that in a right triangle the sum of the squares of the two smaller sides (called the legs) will equal the square of the longest side (called the hypotenuse).
.
So for this problem the sum of the squares of the legs can be written as:
.
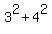
.
and when you square the terms and add them you get:
.

.
For this to be a right triangle that sum, 25, must equal the square of the longest side. The longest side is 5 and 5 squared equals 25 also.
.
So we can say that the Pythagorean theorem holds for Ted's proposed triangle. The sum of the squares of the two legs does equal the square of the longest side and therefore Ted's triangle is a right-triangle because it complies with the Pythagorean theorem.
.
Let's go back to the original requirement and think about it a little more. Why is it true that unless the sum of the two shortest sides is greater than the length of the longest side a triangle cannot be formed? You may already know this, but if not, let's use an example to give you the idea. Suppose we have three lines of dimensions 3, 4, and 10. The rule says that unless the sum of the two shorter sides (3 + 4) is longer than 10, a triangle cannot be formed. So we might suspect that a 3 - 4 - 10 triangle cannot be formed. To demonstrate this, draw a horizontal line of length 10 units (the length of the longest side). Now set a drafting compass so that the distance between the pencil point and the pivot point is 3 units (the length of the shortest side). Put the sharp point on one end of the 10 unit line and use the compass to swing a pencil line circle of radius 3 units around that end of the 10 unit line. Then set the compass for 4 units (the length of the next shorter side). Put the pivot point of the compass at the other end of the 10 unit line and make a pencil line circle of 4 units radius around that end of the 10 unit line. Can you now see that the two circles do not intersect? The 3 unit line will never be able to cross the 4 unit line and form a triangle with the 10 unit line as the longest side. However, you can shorten the 10 unit line to make the longest side say 6 units long (which is a length less than 3 + 4 units). Then you make circle of radius 3 units at one end of the 6 unit line and a circle of radius 4 units at the other end and you will see that the two circles intersect. By drawing a line from one end of the 6 unit line to a point where the two circles intersect and then drawing a line from the other end of the 6 unit line to the same intersection point you will have a 3 - 4 - 6 triangle. Maybe this will help you to understand and remember that this rule of side lengths is a requirement for a triangle.
.
Here's a caution, however. Suppose you are given two sides of lengths 3 and 4. Can you have the third side equal to 1? The answer is "no" and the reason is that 4 is now the longest side, so that the two shortest sides (3 and 1) must have a sum that is greater than (not just equal to, but greater than) 4.
.
Hope this helps you to understand a little more about triangles.
.
|
|
|